题目内容
 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA交AB于点D
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA交AB于点D(1)求证:∠DOC=∠BDO;
(2)若⊙O的半径为4,求阴影部分的面积.(结果保留)
考点:切线的性质,扇形面积的计算
专题:
分析:(1)根据切线的性质定理得到直角三角形,从而根据HL证明直角三角形全等,即可得到对应角相等;
(2)阴影部分的面积=直角△AOB的面积-直角△ACD的面积-扇形OBC的面积.
(2)阴影部分的面积=直角△AOB的面积-直角△ACD的面积-扇形OBC的面积.
解答:(1)证明:∵AB切⊙O于点B,
∴OB⊥AB,即∠B=90°.
又∵DC⊥OA,
∴∠OCD=90°.
在Rt△COD与Rt△BOD中,
,
∴Rt△COD≌Rt△BOD(HL),
∴∠CDO=∠BDO.
(2)解:在Rt△AOB中,∠A=30°,OB=4,
∴OA=8,
AC=OA-OC=8-4=4.
在Rt△ACD中,tan∠A=
,
又∵∠A=30°,AC=4,
∴CD=AC•tan30°=
,
∴S四边形OCDB=2S△OCD=2×
×4×
=
,
又∵∠A=30°,
∴∠BOC=60°.
∴S扇形OBC=
=
∴S阴影=S四边形OCDB-S扇形OBC=
-
.
∴OB⊥AB,即∠B=90°.
又∵DC⊥OA,
∴∠OCD=90°.
在Rt△COD与Rt△BOD中,
|
∴Rt△COD≌Rt△BOD(HL),
∴∠CDO=∠BDO.
(2)解:在Rt△AOB中,∠A=30°,OB=4,
∴OA=8,
AC=OA-OC=8-4=4.
在Rt△ACD中,tan∠A=
| CD |
| AC |
又∵∠A=30°,AC=4,
∴CD=AC•tan30°=
4
| ||
| 3 |
∴S四边形OCDB=2S△OCD=2×
| 1 |
| 2 |
4
| ||
| 3 |
16
| ||
| 3 |
又∵∠A=30°,
∴∠BOC=60°.
∴S扇形OBC=
| 60π×42 |
| 360 |
| 8π |
| 3 |
∴S阴影=S四边形OCDB-S扇形OBC=
16
| ||
| 3 |
| 8π |
| 3 |
点评:本题考查了切线的性质,能够根据切线的性质定理发现直角三角形,熟练运用HL判定直角三角形全等,能够把不规则图形的面积转化为规则图形的面积进行计算是解题关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知抛物线y=a(x-2)2+6经过点(3,3).
(1)求a的值;
(2)求方程a(x-2)2+6=0的解;
(3)若点A(m,y1),B(n,y2)都在该抛物线上,且2<n<m,试比较y1与y2的大小.
(1)求a的值;
(2)求方程a(x-2)2+6=0的解;
(3)若点A(m,y1),B(n,y2)都在该抛物线上,且2<n<m,试比较y1与y2的大小.
 如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )
如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )| A、33° | B、57° |
| C、123° | D、147° |
如果一个n边形每个外角都是30°,那么n的值是( )
| A、11 | B、12 | C、13 | D、14 |
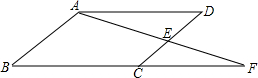 如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为
如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为 填空:如图,已知∠EFD=∠BCA,BC=EF,AF=DC,则AB=DE,请说明理由.
填空:如图,已知∠EFD=∠BCA,BC=EF,AF=DC,则AB=DE,请说明理由. 根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q.
根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q. 如图,在矩形ABCD中放两张面积分别为9和3的正方形纸片,问:矩形ABCD至少有多大面积没有被盖住?
如图,在矩形ABCD中放两张面积分别为9和3的正方形纸片,问:矩形ABCD至少有多大面积没有被盖住?