题目内容
如图①,AB=CD,AD=BC.O为AC中点,过O点的直线分别与AD,BC相交于点M,N.
(1)那么∠1与∠2有什么关系?AM,CN有什么关系?请说明理由.
(2)若将过O点的直线旋转至图②③的情况时,其他条件不变,那么①中的关系还成立吗?请说明理由.

(1)那么∠1与∠2有什么关系?AM,CN有什么关系?请说明理由.
(2)若将过O点的直线旋转至图②③的情况时,其他条件不变,那么①中的关系还成立吗?请说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)如图(1),证明AM∥CN,得到△AMO∽△CNO;进而得到∠1=∠2,
=
;结合AO=CO,即可解决问题.
(2)如图(2),运用与(1)中,类似的方法,证明证明AM∥CN,得到△AMO∽△CNO;进而得到∠1=∠2,
=
;结合AO=CO,即可解决问题.
| AM |
| CN |
| AO |
| CO |
(2)如图(2),运用与(1)中,类似的方法,证明证明AM∥CN,得到△AMO∽△CNO;进而得到∠1=∠2,
| AM |
| CN |
| AO |
| CO |
解答: 解;(1)∵AB=CD,AD=BC,
解;(1)∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,
∴AM∥CN,△AMO∽△CNO
∴∠1=∠2;
=
,
∵AO=CO,
∴AM=CN.
(2)在图(2)、(3)两种情况下,
(1)中的结论仍然成立.
仅以图(2)说明如下:∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,
∴AD∥BC,△AMO∽△CNO
∴∠1=∠2;
=
,
∵AO=CO,
∴AM=CN.
 解;(1)∵AB=CD,AD=BC,
解;(1)∵AB=CD,AD=BC,∴四边形ABCD为平行四边形,
∴AM∥CN,△AMO∽△CNO
∴∠1=∠2;
| AM |
| CN |
| AO |
| CO |
∵AO=CO,
∴AM=CN.
(2)在图(2)、(3)两种情况下,
(1)中的结论仍然成立.
仅以图(2)说明如下:∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,
∴AD∥BC,△AMO∽△CNO
∴∠1=∠2;
| AM |
| CN |
| AO |
| CO |
∵AO=CO,
∴AM=CN.
点评:该题主要考查了全等三角形的判定、平行四边形的判定等几何知识点及其应用问题;解题的关键是牢固掌握定理本质内容,灵活运用动态的观念,来观察、分析、运动图形中的不变元素.

练习册系列答案
相关题目
多项式2x4-5x3+x2+5x-3中不可能含有的因式是( )
| A、x+1 | B、x-1 |
| C、x-2 | D、2x-3 |
 如图,长春市某中学学生小刚在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得窗户A处到底面的距离AB为20米,树顶C处的俯角为44°,楼底到大树的距离BD为12米,求树CD的高度.(保留小数点后一位,参考数据:sin44°≈0.69,cos44°≈0.72,tan44°≈0.97)
如图,长春市某中学学生小刚在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得窗户A处到底面的距离AB为20米,树顶C处的俯角为44°,楼底到大树的距离BD为12米,求树CD的高度.(保留小数点后一位,参考数据:sin44°≈0.69,cos44°≈0.72,tan44°≈0.97)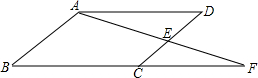 如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为
如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为 根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q.
根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q. 如图,⊙O的弦AB垂直于弦CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到AB的距离是
如图,⊙O的弦AB垂直于弦CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到AB的距离是