题目内容
 已知:如图,AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C.
已知:如图,AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C.求证:(1)AE=CF;(2)AE∥CF.
考点:全等三角形的判定与性质,平行线的判定与性质
专题:证明题
分析:(1)要证AE=CF,只需证到△ABE≌△CDF即可;
(2)由△ABE≌△CDF可得∠AEB=∠CFD,然后根据等角的补角相等可得∠AED=∠CFB,就可得到AE∥CF.
(2)由△ABE≌△CDF可得∠AEB=∠CFD,然后根据等角的补角相等可得∠AED=∠CFB,就可得到AE∥CF.
解答:解:(1)∵AB∥CD,
∴∠B=∠D.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AE=CF;
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD.
∵∠AEB+∠AED=180°,∠CFD+∠CFB=180°,
∴∠AED=∠CFB,
∴AE∥CF.
∴∠B=∠D.

在△ABE和△CDF中,
|
∴△ABE≌△CDF(ASA),
∴AE=CF;
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD.
∵∠AEB+∠AED=180°,∠CFD+∠CFB=180°,
∴∠AED=∠CFB,
∴AE∥CF.
点评:本题主要考查了平行线的判定与性质、全等三角形的判定与性质、等角的补角相等等知识,证明△ABE≌△CDF是解决本题的关键.

练习册系列答案
相关题目
 如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )
如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )| A、33° | B、57° |
| C、123° | D、147° |
如果一个n边形每个外角都是30°,那么n的值是( )
| A、11 | B、12 | C、13 | D、14 |
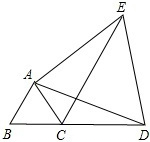 如图所示,△ABC为等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边△ADE.连接CE.求证:CE=AC+CD.
如图所示,△ABC为等边三角形,D是BC延长线上一点,连接AD,以AD为边作等边△ADE.连接CE.求证:CE=AC+CD. 如图,图中有哪些同位角,内错角,同旁内角?并写出(至少各写出四对)
如图,图中有哪些同位角,内错角,同旁内角?并写出(至少各写出四对) 在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.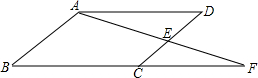 如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为
如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为 填空:如图,已知∠EFD=∠BCA,BC=EF,AF=DC,则AB=DE,请说明理由.
填空:如图,已知∠EFD=∠BCA,BC=EF,AF=DC,则AB=DE,请说明理由.