题目内容
如图，在△ABC中，AB=13，AC=15，BC=14，求sinB和sinC的值．考点：解直角三角形
专题：计算题
分析：作AD⊥BC于D，如图，设BD=x，AD=y，则CD=14-x，根据勾股定理，在Rt△ABD中有x2+y2=132①，在Rt△ACD中有（14-x）2+y2=152②，再利用②-①消去y可求出x=5，接着把x=5代入①可解得y=12，然后利用正弦的定义求解．
解答：解：作AD⊥BC于D，如图，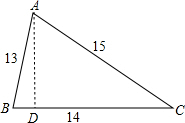
设BD=x，AD=y，则CD=14-x，
在Rt△ABD中，∵BD2+AD2=AB2，
∴x2+y2=132①，
在Rt△ACD中，∵CD2+AD2=AC2，
∴（14-x）2+y2=152②，
②-①得-28x+142=152-132，解得x=5，
把x=5代入①得25+y2=132，解得y=12，
在Rt△ABD中，sinB=
=
；
在Rt△ACD中，sinC=
=
．
设BD=x，AD=y，则CD=14-x，在Rt△ABD中，∵BD2+AD2=AB2，
∴x2+y2=132①，
在Rt△ACD中，∵CD2+AD2=AC2，
∴（14-x）2+y2=152②，
②-①得-28x+142=152-132，解得x=5，
把x=5代入①得25+y2=132，解得y=12，
在Rt△ABD中，sinB=
| AD |
| AB |
| 12 |
| 13 |
在Rt△ACD中，sinC=
| AD |
| AC |
| 12 |
| 15 |
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，若BD=1，AD=3，则tan∠BCD=
如图所示，把它折叠成正方体后三组对面上的两个数之和分别相等，则x=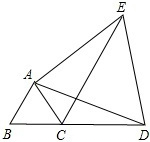
如图所示，△ABC为等边三角形，D是BC延长线上一点，连接AD，以AD为边作等边△ADE．连接CE．求证：CE=AC+CD．
如图，长春市某中学学生小刚在自家楼房的窗户A处，测量楼前的一棵树CD的高．现测得窗户A处到底面的距离AB为20米，树顶C处的俯角为44°，楼底到大树的距离BD为12米，求树CD的高度．（保留小数点后一位，参考数据：sin44°≈0.69，cos44°≈0.72，tan44°≈0.97）
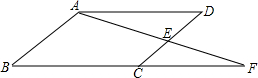如图，在?ABCD中，E为CD的中点，连结AE并延长交BC的延长线于点F，则△ADE与△ABF的面积比为