题目内容
 如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,
如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,(1)若AB=CD,∠A=∠C,求证:FM=EM;
(2)若AB=CD,FM=EM,求证:∠A=∠C.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由条件可先证明△ABF≌△CDE,可得BF=DE,再证明△BFM≌△DEM,可得到FM=EM;
(2)由条件可先证明△BFM≌△DEM,可得BF=DE,再证明△ABF≌△DEM,可得∠A=∠C.
(2)由条件可先证明△BFM≌△DEM,可得BF=DE,再证明△ABF≌△DEM,可得∠A=∠C.
解答:证明:
(1)∵BF⊥AC,DE⊥AC,
∴∠AFB=∠CED,
在△ABF和△CDE中
∴△ABF≌△CDE(AAS),
∴BF=DE,
在△BFM和△DEM中
∴△BFM≌△DEM(AAS),
∴FM=EM;
(2)∵BF⊥AC,DE⊥AC,
∴∠BFM=∠DEM=90°,
在△BFM和△DEM中
∴△BFM≌△DEM(ASA),
∴BF=DE,
在Rt△ABF和Rt△CDE中
∴△ABF≌△CDE(HL),
∴∠A=∠C.
(1)∵BF⊥AC,DE⊥AC,
∴∠AFB=∠CED,
在△ABF和△CDE中
|
∴△ABF≌△CDE(AAS),
∴BF=DE,
在△BFM和△DEM中
|
∴△BFM≌△DEM(AAS),
∴FM=EM;
(2)∵BF⊥AC,DE⊥AC,
∴∠BFM=∠DEM=90°,
在△BFM和△DEM中
|
∴△BFM≌△DEM(ASA),
∴BF=DE,
在Rt△ABF和Rt△CDE中
|
∴△ABF≌△CDE(HL),
∴∠A=∠C.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )
如图,已知∠1=∠2=90°,∠3=123°,则∠4等于( )| A、33° | B、57° |
| C、123° | D、147° |
 如图所示,把它折叠成正方体后三组对面上的两个数之和分别相等,则x=
如图所示,把它折叠成正方体后三组对面上的两个数之和分别相等,则x=
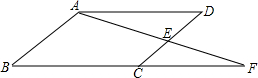 如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为
如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为 根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q.
根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q. 如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.
如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.