题目内容
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF长的最小值是考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;求出DF、AD的长度,即可解决问题.
解答: 解:由题意得:DF=DB,
解:由题意得:DF=DB,
∴点F在以D为圆心,BD为半径的圆上,作⊙D; 连接AD交⊙D于点F,此时AF值最小;
∵点D是边BC的中点,
∴CD=BD=3;而AC=4,
由勾股定理得:AD2=AC2+CD2
∴AD=5,而FD=3,
∴FA=5-3=2,
即线段AF长的最小值是2.
故答案为2.
 解:由题意得:DF=DB,
解:由题意得:DF=DB,∴点F在以D为圆心,BD为半径的圆上,作⊙D; 连接AD交⊙D于点F,此时AF值最小;
∵点D是边BC的中点,
∴CD=BD=3;而AC=4,
由勾股定理得:AD2=AC2+CD2
∴AD=5,而FD=3,
∴FA=5-3=2,
即线段AF长的最小值是2.
故答案为2.
点评:该题主要考查了翻折变换的性质、勾股定理、最值问题等几何知识点及其应用问题;解题的关键是作辅助线,从整体上把握题意,准确找出图形中数量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果一个n边形每个外角都是30°,那么n的值是( )
| A、11 | B、12 | C、13 | D、14 |

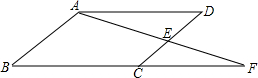 如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为
如图,在?ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,则△ADE与△ABF的面积比为 根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q.
根据程序设定,机器人在平面上能完成下列动作:如图,先从点O沿北偏东60°方向行走一段时间到点P后,立即再向正北方向行走一段时间到点Q.但何时改变方向不定,假设机器人行走速度为2m/min,机器人行走3min时到达的位置为点Q. 如图,⊙O的弦AB垂直于弦CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到AB的距离是
如图,⊙O的弦AB垂直于弦CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到AB的距离是 如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.
如图,已知点B,C分别在射线AN,AM上,∠MCB与∠NBC的平分线交于点P.