题目内容
5.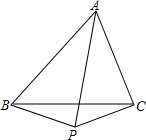 如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.
分析 作PE⊥AB于E,PF⊥AC交AC的延长线于F,根据线段垂直平分线的性质得到PB=PC,根据角平分线的性质,得到PE=PF,证明Rt△PEB≌Rt△PFC即可.
解答 答:∠ABP+∠ACP=180°,
证明: 作PE⊥AB于E,PF⊥AC交AC的延长线于F,
作PE⊥AB于E,PF⊥AC交AC的延长线于F,
∵AP是∠BAC的平分线,PE⊥AB,PF⊥AC,
∴PE=PF,
∵点P在BC的垂直平分线上,
∴PB=PC,
在Rt△PEB和Rt△PFC中,
$\left\{\begin{array}{l}{PE=PF}\\{PB=PC}\end{array}\right.$,
∴Rt△PEB≌Rt△PFC,
∴∠ABP=∠FCP,又∠FCP+∠ACP=180°,
∴ABP+∠ACP=180°.
点评 本题考查的是线段垂直平分线的性质和角平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等、角平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
17.南浔粮食批发市场A、B两个摊主得知练市和双林两个城镇急需粮食240吨和260吨的消息后,决定向两个城镇调运粮食.已知A摊主有粮食200吨,B摊主有粮食300吨,现将这些粮食全部调往两个城镇.从A摊主运往两城镇的费用分别为每吨20元和25元,B摊主运往两个城镇的费用分别为每吨15元和18元.设从B摊主运往练市的粮食为x吨.
(1)请填写下表,并求两个摊主调运粮食的运费相等时的x的值;
(2)设A、B两个摊主的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案.
(1)请填写下表,并求两个摊主调运粮食的运费相等时的x的值;
| 练市 | 双林 | 总计 | |
| A | (240-x)吨 | (x-40)吨 | 200吨 |
| B | x吨 | (300-x)吨 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
14.三角形的三边长为(a-b)2=c2-2ab,则这个三角形是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 等边三角形 |
 已知:∠MON=40°,OE平分∠MON.
已知:∠MON=40°,OE平分∠MON. 如图,在正方形ABCD中,点G是BC延长线一点,连接AG,分别交BD、CD于点E、F.
如图,在正方形ABCD中,点G是BC延长线一点,连接AG,分别交BD、CD于点E、F. 如图,第四象限的角平分线OA与反比例函数y=$\frac{k}{x}$的图象交于点A,已知OA=3$\sqrt{2}$,则该函数的解析式为y=$\frac{-9}{x}$.
如图,第四象限的角平分线OA与反比例函数y=$\frac{k}{x}$的图象交于点A,已知OA=3$\sqrt{2}$,则该函数的解析式为y=$\frac{-9}{x}$.