题目内容
15.计算题(1)xy2•(-x2y)3÷(-x2y2)
(2)(a+b-c)(a-b+c)
(3)[(x+2y)2-(x+y)(3x-y)-5y2]÷2x.
分析 (1)原式先计算乘方运算,再计算乘除运算即可得到结果;
(2)原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
(3)原式中括号中利用完全平方公式,多项式乘以多项式法则计算,去括号合并后利用多项式除以单项式法则计算即可得到结果.
解答 解:(1)原式=xy2•(-x6y3)÷(-x2y2)=x5y3;
(2)原式=a2-(b-c)2=a2-b2+2bc-c2;
(3)原式=(x2+4xy+4y2-3x2-2xy+y2-5y2)÷2x=(-2x2+2xy)÷2x=-x+y.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | (-4m2)3=-4m6 | B. | ${(-\frac{1}{2})^{-4}}+{(π-3)^0}$=16 | ||
| C. | (a+b)2=(a-b)2+4ab | D. | $9{x^3}{y^2}÷(-\frac{1}{3}{x^3}y)=-3y$ |
20.要使分式$\frac{x}{x-1}$有意义,则x应满足的条件是( )
| A. | x≠1 | B. | x≠1或x≠0 | C. | x≠0 | D. | x>1 |
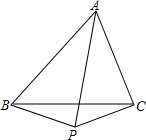 如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.