题目内容
20. 如图,在正方形ABCD中,点G是BC延长线一点,连接AG,分别交BD、CD于点E、F.
如图,在正方形ABCD中,点G是BC延长线一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;
(2)当∠G=30°时,求$\frac{DF}{FC}$的值.
分析 (1)通过全等三角形的判定定理SAS判定△DAE≌△DCE,然后根据全等三角形的对应角相等知∠DAE=∠DCE;
(2)设正方形ABCD的边长为a,由已知条件可求出DF,CF的长,进而可求出其比值.
解答 (1)证明:∵四边形ABCD是正方形,BD是对角线,
∴∠ADE=∠CDE(正方形的对角线平分对角),AD=DC,
在△DAE和△DCE中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADE=∠CDE}\\{DE=DE}\end{array}\right.$,
∴△DAE≌△DCE (SAS),
∴∠DAE=∠DCE(全等三角形的对应角相等);
(2)∵四边形ABCD是正方形,
∴∠ADF=∠FCG=90°,AD∥BC,
设正方形边长为a,
∵∠G=30°,
∴∠DAF=30°,
∴DF=$\frac{\sqrt{3}}{3}$a,
∴CF=DC-DF=a-$\frac{\sqrt{3}}{3}$a=$\frac{3-\sqrt{3}}{3}$a,
∴$\frac{DF}{CF}$=$\frac{\sqrt{3}+1}{2}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的性质及特殊角的三角函数值,本题综合比较强,考查了学生对于知识的综合运用能力.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | (-4m2)3=-4m6 | B. | ${(-\frac{1}{2})^{-4}}+{(π-3)^0}$=16 | ||
| C. | (a+b)2=(a-b)2+4ab | D. | $9{x^3}{y^2}÷(-\frac{1}{3}{x^3}y)=-3y$ |
12.一元二次方程3x2-4x=5的二次项系数是( )
| A. | 3 | B. | -4 | C. | 5 | D. | -5 |
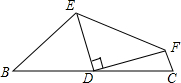 如图,四边形BEFC中D为BC的中点,∠EDF=90°,求证:BE+FC>EF.
如图,四边形BEFC中D为BC的中点,∠EDF=90°,求证:BE+FC>EF.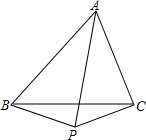 如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.