题目内容
15.已知关于x的一元二次方程2x2-mx-2m+1=0的两根的平方和是$\frac{29}{4}$,求m的值.分析 首先设关于x的一元二次方程2x2-mx-2m+1=0的两个实数根分别为x1,x2,然后根据根与系数的关系,即可得x1+x2=$\frac{m}{2}$,x1•x2=$\frac{-2m+1}{2}$,又由于x的一元二次方程2x2-mx-2m+1=0的两根的平方和是$\frac{29}{4}$,即可得出关于m的方程,解此方程即可求得答案.
解答 解:设关于x的一元二次方程2x2-mx-2m+1=0的两个实数根分别为x1,x2,
则:x1+x2=$\frac{m}{2}$,x1•x2=$\frac{-2m+1}{2}$,
∵关于x的一元二次方程2x2-mx-2m+1=0的两个实数根的平方和为$\frac{29}{4}$,
∴x12+x22=(x1+x2)2-2x1•x2=($\frac{m}{2}$)2-2×$\frac{-2m+1}{2}$=$\frac{29}{4}$,
解得:m1=3,m2=-11,
当m=3时,△=m2-8(-2m+1)=49>0,
当m=-11时,△=m2-8(-2m+1)=-63<0(舍去),
∴m=3.
点评 此题考查了一元二次方程根与系数的关系以及完全平方式的应用.此题难度不大,解题的关键是掌握:若二次项系数为1,常用以下关系:x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q性质的应用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
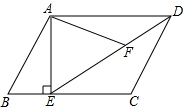 如图,在?ABCD中,E为BC边上一点,连接AE、DE,F为线段DE上一点,且∠AFE=∠B.试说明△ADF∽△DEC.
如图,在?ABCD中,E为BC边上一点,连接AE、DE,F为线段DE上一点,且∠AFE=∠B.试说明△ADF∽△DEC. 已知,如图所示,在△ABC中,AB>AC,∠ABC的平分线与∠ACB的平分线相交于O点,猜想OB与OC的大小关系.
已知,如图所示,在△ABC中,AB>AC,∠ABC的平分线与∠ACB的平分线相交于O点,猜想OB与OC的大小关系.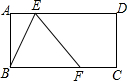 在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.
在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.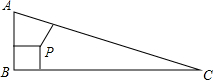 如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )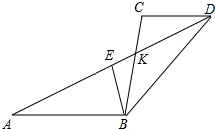 如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.
如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.