题目内容
7.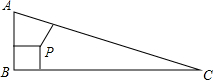 如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离是( )| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
分析 连接AP,BP,CP,根据勾股定理求得AC的长,再根据直角三角形的面积公式即可求得该距离的长.
解答  解:连接AP,BP,CP
解:连接AP,BP,CP
设PE=PF=PG=x,
∵AB=7,BC=24,
∴AC=$\sqrt{{7}^{2}+2{4}^{2}}$=25,
再根据直角三角形的面积,S△ABC=$\frac{1}{2}$×AB×CB=84,
S△ABC=$\frac{1}{2}$AB×x+$\frac{1}{2}$AC×x+$\frac{1}{2}$BC×x=$\frac{1}{2}$(AB+BC+AC)•x=$\frac{1}{2}$×56x=28x,
∴28x=84,
解得:x=3,
故选B.
点评 本题主要考查直角三角形的内切圆的性质、角平分线的性质等知识点,关键在于分析出这个距离就是求这个三角形的内切圆的半径.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
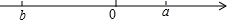 如图,已知数轴上表示数a、b的点:
如图,已知数轴上表示数a、b的点: