题目内容
10. 已知,如图所示,在△ABC中,AB>AC,∠ABC的平分线与∠ACB的平分线相交于O点,猜想OB与OC的大小关系.
已知,如图所示,在△ABC中,AB>AC,∠ABC的平分线与∠ACB的平分线相交于O点,猜想OB与OC的大小关系.
分析 先根据角平分线的性质得出∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,再由AB>AC可知∠ACB>∠ABC,故可得出∠OCB>∠OBC,由此可得出结论.
解答 解:∵∠ABC的平分线与∠ACB的平分线相交于O点,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB.
∵AB>AC,
∴∠ACB>∠ABC,
∴∠OCB>∠OBC,
∴OB>OC.
点评 本题考查的是三角形内角和定理,熟知角平分线的性质是解答此题的关键.

练习册系列答案
相关题目
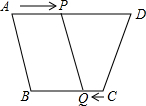 梯形ABCD中AD∥BC且AB=DC,AD=10cm,BC=6cm,P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,Q以4cm/s的速度由C出发向B运动,问:
梯形ABCD中AD∥BC且AB=DC,AD=10cm,BC=6cm,P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,Q以4cm/s的速度由C出发向B运动,问: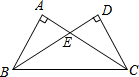 如图,∠A=∠D=90°,要使△ABC≌△DCB,只需要增加:①AB=DC;②AC=DB;③BC=BC;④∠ABC=∠DCB;⑤∠ACB=∠DBC中的一个条件①②④⑤(只需填写一个正确的条件).
如图,∠A=∠D=90°,要使△ABC≌△DCB,只需要增加:①AB=DC;②AC=DB;③BC=BC;④∠ABC=∠DCB;⑤∠ACB=∠DBC中的一个条件①②④⑤(只需填写一个正确的条件).