题目内容
20. 在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.
在矩形ABCD中,AB=3,BC=6,将矩形折叠,使B点落在AD(含端点)上,落点记为E,这时折痕与边BC(含端点)交于F,然后展开铺平,则以B、E、F为顶点的△BEF,称为矩形ABCD的“折痕三角形”.当折痕△BEF的面积最大时,AE的长为6-3$\sqrt{3}$.
分析 当点F与点C重合时,△BEF的面积有最大值,设AE=x,则DE=6-x,由折叠的性质可知:EC=BC=6,在Rt△EDC中,利用勾股定理可得到关于x的方程,然后解方程即可求得AE的长.
解答 解:如图所示: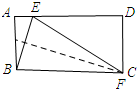
设AE=x,则ED=6-x,由折叠的性质可知EC=CB=6.
在Rt△EDC中,由勾股定理得:ED2+DC2=EC2,即:(6-x)2+32=62,
解得:x1=6-3$\sqrt{3}$,x2=6+3$\sqrt{3}$(舍去).
∴AE=6-3$\sqrt{3}$.
故答案为:6-3$\sqrt{3}$.
点评 本题主要考查的翻折的性质、勾股定理的应用,根据翻折的性质求得EC的长度,然后在Rt△EDC中,由勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
9.数轴上点M到1的距离是5,则点M表示的数是( )
| A. | 6 | B. | -4 | C. | 6或-4 | D. | 不能确定 |
10.P是∠B的角平分线和∠C的角平分线在△ABC内的交点,∠BPC=120°,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |