题目内容
20．已知|m|=4，|n|=6，且|m+n|=m+n，求m-n的值．分析 首先根据绝对值的性质得到m、n的值，然后再根据绝对值的性质确定m、n的值，进而可得m-n的值．
解答 解：∵|m|=4，|n|=6，
∴m=±4，n=±6，
∵|m+n|=m+n，
∴m+n≥0，
∴m=±4，n=6，
∴当m=4，n=6时，m-n=-2，
当m=-4，n=6时，m-n=-10，
综上：m-n=-2或-10．
点评 此题主要考查了有理数的减法，以及绝对值的性质，关键是掌握绝对值等于一个正数的数有两个，它们互为相反数．
练习册系列答案
相关题目
11．$\frac{{a}^{2}+a-2}{{a}^{2}+3a+2}$•5（a+1）2等于（ ）
| A． | a2+2a+1 | B． | 5a2+10 a+5 | C． | 5a2-1 | D． | 5a2-5 |
8．下列是二元一次方程组$\left\{\begin{array}{l}{x-y=1}\\{2x+y=2}\end{array}\right.$的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$ |
15．将正整数依次按如表规律排成4列，根据表中的排列规律，数2016应在（ ）
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
| A． | 第671行第2列 | B． | 第671行第3列 | C． | 第672行第2列 | D． | 第672行第3列 |
在平面直角坐标系中，有点A（2，0），B（0，3），C（0，2），点D在第二象限，且△AOB≌△OCD．请在图中画出△OCD，并直接写出点D的坐标：D （-3，2）．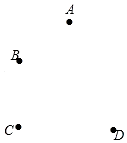
如图，平面上四个点A，B，C，D．按要求完成下列问题：