题目内容
9.如果关于的方程x2+3x-a=0有两个相等的实数根,那么a=-$\frac{9}{4}$.分析 根据方程x2+3x-a=0有两个相等的实数根可得△=32-4(-a)=9+4a=0,求出a的值即可.
解答 解:∵关于的方程x2+3x-a=0有两个相等的实数根,
∴△=0,
∴32-4(-a)=9+4a=0,
∴a=-$\frac{9}{4}$,
故答案为:-$\frac{9}{4}$.
点评 本题主要考查了根的判别式的知识,解答本题的关键是掌握一元二次方程根的情况与判别式△的关系:△=0?方程有两个相等的实数根,此题难度不大.

练习册系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{2x+1≥0}\\{x-1<0}\end{array}\right.$的解集是( )
| A. | x≥-$\frac{1}{2}$ | B. | x<1 | C. | -$\frac{1}{2}$≤x<1 | D. | -$\frac{1}{2}$<x<1 |
19.下列式子正确的是( )
| A. | ($\sqrt{-2}$)2=2 | B. | $\sqrt{(-5)^{2}}$=-5 | C. | $\sqrt{(-6)^{2}}$=6 | D. | (3$\sqrt{2}$)2=6 |
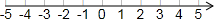 解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$
解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$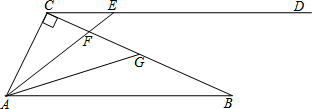
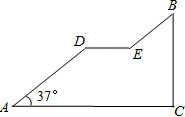 如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.
如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.