题目内容
19.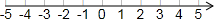 解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$
解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1≥x②}\end{array}\right.$请结合题意填空,完成本题的解答
(1)解不等式①,得x>3
(2)解不等式②,得x≥1
(3)把不等式①和②的解集在数轴上表示出来
(4)原不等式组的解集为x>3.
分析 根据不等式组分别求出x的取值范围,然后画出数轴,数轴上相交的点的集合就是该不等式的解集.若没有交集,则不等式无解.
解答 解:(1)解不等式①,得x>3,
(2)解不等式②,得x≥1,
(3)把不等式①和②的解集在数轴上表示出来是:
(4)原不等式组的解集为x>3.
故答案为:x>3,x≥1,x>3.
点评 此题考查了一元一次不等式解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
10.某车间5月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2,3,1,1.则在这10天中该车间生产零件的次品数的( )
| A. | 众数是3 | B. | 中位数是1.5 | C. | 平均数是2 | D. | 以上都不正确 |
14.第六次全国人口普查数据显示,天津市宝坻区常住人口均为79.9万人,79.9万用科学记数法表示正确的是( )
| A. | 79.9×108 | B. | 7.99×108 | C. | 7.99×105 | D. | 0.799×106 |
11.下列运算正确的是( )
| A. | a3+a2=a5 | B. | 3a2-a2=22 | C. | a3•a2=a5 | D. | a6÷a3=a2 |
 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似? 如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为20cm.
如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为20cm.