题目内容
1.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,如果CD=4,BD=3,那么∠A的正弦值是$\frac{3}{5}$.分析 求出∠A=∠BCD,根据锐角三角函数的定义求出sin∠BCD即可.
解答 解: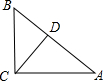
∵CD⊥AB,
∴∠CDB=90°,
由勾股定理得:BC=5,
∵∠ACB=90°,
∴∠A+∠B=90°,∠BCD+∠B=90°,
∴∠A=∠BCD,
∴sinA=sin∠BCD=$\frac{BD}{BC}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解此题的关键,注意:在Rt△ACB中,∠ACB=90°,则sinA=$\frac{BC}{AB}$,cosA=$\frac{AC}{AB}$,tanA=$\frac{BC}{AC}$.

练习册系列答案
相关题目
10.已知a>b,下列关系式中一定正确的是( )
| A. | a2<b2 | B. | 2a<2b | C. | a+2<b+2 | D. | -a<-b |
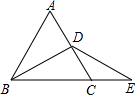 如图,等边△ABC的周长是12,D是AC边上的中点,E在BC的延长线上,若DE=DB,则CE的长为2.
如图,等边△ABC的周长是12,D是AC边上的中点,E在BC的延长线上,若DE=DB,则CE的长为2.
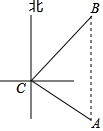 如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.
如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.