题目内容
11.如果点A(-1,4)、B(m,4)在抛物线y=a(x-1)2+h上,那么m的值为3.分析 根据函数值相等两点关于对称轴对称,可得答案.
解答 解:由点A(-1,4)、B(m,4)在抛物线y=a(x-1)2+h上,得
(-1,4)与(m,4)关于对称轴x=1对称,
m-1=1-(-1),
解得m=3,
故答案为:3.
点评 本题考查了二次函数图象上点的坐标特征,利用函数值相等两点关于对称轴对称得出m-1=1-(-1)是解题关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
6.将抛物线y=ax2-1平移后与抛物线y=a(x-1)2重合,抛物线y=ax2-1上的点A(2,3)同时平移到A′,那么点A′的坐标为( )
| A. | (3,4) | B. | (1,2) | C. | (3,2) | D. | (1,4) |
3.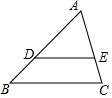 如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )
如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )
 如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )
如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )| A. | AD•DB=AE•EC | B. | AD•AE=BD•EC | C. | AD•CE=AE•BD | D. | AD•BC=AB•DE |
1.体育比赛中,所有13位参赛者的成绩互不相同,在已知自己成绩的情况下,要想知道自己是否进入前6名,只需要知道所有参赛者成绩的( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
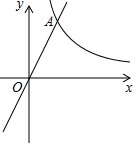 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.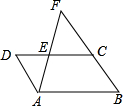 如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F;
如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F;