Question

6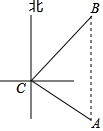．如图，一艘海轮位于小岛C的南偏东60°方向，距离小岛120海里的A处，该海轮从A处正北方向航行一段距离后，到达位于小岛C北偏东45°方向的B处．
（1）求该海轮从A处到B处的航行过程中与小岛C之间的最短距离（记过保留根号）；
（2）如果该海轮以每小时20海里的速度从B处沿BC方向行驶，求它从B处到达小岛C的航行时间（结果精确到0.1小时）．（参考数据：$\sqrt{2}$=1.41，$\sqrt{3}$=1.73）

Answer 1

分析 （1）首先过点C作CD⊥AB于D，构建直角△ACD，通过解该直角三角形得到CD的长度即可；
（2）通过解直角△BCD来求BC的长度．

解答 解：（1）如图，过点C作CD⊥AB于D，
由题意，得∠ACD=30°．
在直角△ACD中，∠ADC=90°，
∴cos∠ACD=$\frac{AD}{AC}$，
∴CD=AC•cos30°=120×$\frac{\sqrt{3}}{2}$=60$\sqrt{3}$（海里）；

（2）在直角△BCD中，∠BDC=90°，∠DCA=45°，
∴cos∠BCD=$\frac{CD}{BC}$，
∴BC=$\frac{CD}{cos45°}$=$\frac{60\sqrt{3}}{\frac{\sqrt{2}}{2}}$=60$\sqrt{6}$≈60×2.44=146.4（海里），
∴146.4÷20=7.32≈7.3（小时）．
答：（1）求该海轮从A处到B处的航行过程中与小岛C之间的最短距离是60$\sqrt{3}$海里；
（2）如果该海轮以每小时20海里的速度从B处沿BC方向行驶，求它从B处到达小岛C的航行时间约为7.3小时．

点评 此题考查了方向角问题．此题难度适中，注意将方向角问题转化为解直角三角形的知识求解是解此题的关键，注意数形结合思想的应用．