题目内容
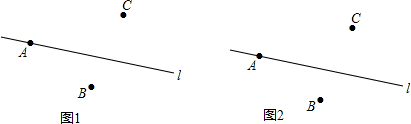
3.如图,A,B,C是同一平面内的三点,且A与B距离为5,B与C距离为6,A与C距离为8,直线l经过点A,且可以绕点A转动,点P是直线l上的任意一点.(1)若直线l与线段BC有交点,在图1中画出使BP+PC取最小值的点P,并写出BP+PC的最小值;
(2)如图2.
①若图中表示的是直线l的一个确定的位置,画图表示线段BP长度最小的位置,并说明理由;
②当直线l绕点A转动时,设点B到直线l的距离的最大值为m,直接写出m的值.
分析 (1)根据线段公理即可求解;
(2)①根据垂线段最短即可求解;
②点B到直线l的距离的最大值即为A与B距离;依此即可求解.
解答 解:(1)如图1,BP+PC的最小值是BC=6;
(2)①如图2,理由:垂线段最短;
②m的值为AB=5.
点评 考查了线段的性质,关键是熟悉两点之间线段最短,垂线段最短的知识点.

练习册系列答案
相关题目
11. 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )| A. | 8056 | B. | 8050 | C. | 8054 | D. | 8052 |
15.若tan40°=a,则tan50°=( )
| A. | $\frac{1}{a}$ | B. | -a | C. | a | D. | 2a |
12. 已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
 已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )| A. | 函数值y随x的增大而减少 | B. | kb<0 | ||
| C. | 当x<1时,y>0 | D. | k+b<0 |
 如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).
如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).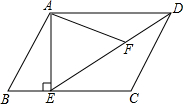 如图,在平行四边形ABCD中,过点A作AE⊥BE,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BE,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.