题目内容
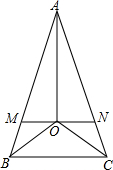 如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB,AC于M,N,连接AO.
如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB,AC于M,N,连接AO.(1)证明:△BOC是等腰三角形.
(2)BM与CN相等吗?对你的结论说明理由.
(3)证明:AO⊥MN.
考点:等腰三角形的判定与性质
专题:
分析:(1)根据角平分线的性质得到∠OBC=∠OCB,即可得到答案.
(2)根据角平分线的定义可得∠MBO=∠CBO,再根据两直线平行,内错角相等可得∠CBO=∠MOB,从而得到∠MBO=∠MOB,即可得证;
(3)先由AB=AC得出∠ABC=∠ACB,再根据BN、CN分别平分∠ABC,∠ACB得出∠OBC=∠OCB,故△ABO≌△ACO,所以MO=NO,再由AB=AC即可得出结论.
(2)根据角平分线的定义可得∠MBO=∠CBO,再根据两直线平行,内错角相等可得∠CBO=∠MOB,从而得到∠MBO=∠MOB,即可得证;
(3)先由AB=AC得出∠ABC=∠ACB,再根据BN、CN分别平分∠ABC,∠ACB得出∠OBC=∠OCB,故△ABO≌△ACO,所以MO=NO,再由AB=AC即可得出结论.
解答:(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
又∵∠B与∠C的角平分线交于点O,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠OBC=∠OCB,
∴OB=OC,
∴△BOC是等腰三角形;
(2)解:BM=CN,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴AB-AM=AC-AN,
即BM=CN;
(3)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BN、CN分别平分∠ABC,∠ACB,
∴∠OBC=∠OCB,
∴BO=CO,
∴△ABO≌△ACO,
∴MO=NO.
∵AB=AC,
∴AO⊥MN.
∴∠ABC=∠ACB,
又∵∠B与∠C的角平分线交于点O,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠OBC=∠OCB,
∴OB=OC,
∴△BOC是等腰三角形;
(2)解:BM=CN,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴∠AMN=∠ANM,
∴AM=AN,
∴AB-AM=AC-AN,
即BM=CN;
(3)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BN、CN分别平分∠ABC,∠ACB,
∴∠OBC=∠OCB,
∴BO=CO,
∴△ABO≌△ACO,
∴MO=NO.
∵AB=AC,
∴AO⊥MN.
点评:本题考查的是等腰三角形的判定与性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知平行四边形ABCD,点E是CD的中点,连结BE并延长与AD的延长线交于F,且与对角线AC交于M.求证:BM•EF=BF•EM.
已知平行四边形ABCD,点E是CD的中点,连结BE并延长与AD的延长线交于F,且与对角线AC交于M.求证:BM•EF=BF•EM.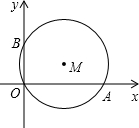 如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.
如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.