题目内容
一个不透明的布袋里装有4个球,其中3个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球.求两次摸出的球恰好颜色相同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为
,求n的值.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球.求两次摸出的球恰好颜色相同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为
| 4 |
| 7 |
考点:列表法与树状图法,概率公式
专题:
分析:(1)由一个不透明的布袋里装有4个球,其中3个红球,1个白球,它们除颜色外其余都相同,然后直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的球恰好颜色相同的情况,再利用概率公式即可求得答案;
(3)根据概率公式可得方程:
=
,解此方程即可求得答案.
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的球恰好颜色相同的情况,再利用概率公式即可求得答案;
(3)根据概率公式可得方程:
| 1+n |
| 4+n |
| 4 |
| 7 |
解答:解:(1)∵一个不透明的布袋里装有4个球,其中3个红球,1个白球,它们除颜色外其余都相同.
∴摸出1个球是白球的概率为:
;
(2)画树状图得:

∵共有16种等可能的结果,两次摸出的球恰好颜色相同的有10种情况,
∴两次摸出的球恰好颜色相同的概率为:
;
(3)由题意得,
=
,
解得,n=3经检验符合题意.
∴摸出1个球是白球的概率为:
| 1 |
| 4 |
(2)画树状图得:

∵共有16种等可能的结果,两次摸出的球恰好颜色相同的有10种情况,
∴两次摸出的球恰好颜色相同的概率为:
| 5 |
| 8 |
(3)由题意得,
| 1+n |
| 4+n |
| 4 |
| 7 |
解得,n=3经检验符合题意.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
化简-(
)2的结果是( )
| a |
| A、a2 | ||
| B、-a | ||
| C、a | ||
D、-
|
 已知平行四边形ABCD,点E是CD的中点,连结BE并延长与AD的延长线交于F,且与对角线AC交于M.求证:BM•EF=BF•EM.
已知平行四边形ABCD,点E是CD的中点,连结BE并延长与AD的延长线交于F,且与对角线AC交于M.求证:BM•EF=BF•EM. 国道通过A,B两村庄,而C村庄离国道较远,为了响应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道.已知C村到A,B两村的距离分别为6km,8km,A,B两村距离为10km,那么这条水泥路的最短距离为多少?
国道通过A,B两村庄,而C村庄离国道较远,为了响应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道.已知C村到A,B两村的距离分别为6km,8km,A,B两村距离为10km,那么这条水泥路的最短距离为多少?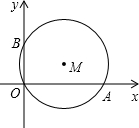 如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根.
如图:⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程x2-17x+60=0的两根. 如图:△ABC是一张直角三角形纸片,其中∠C=90°,BC=8cm,AB=10cm,将纸片折叠,使点A恰好落在BC的中点D处,折痕为MN,试求出AM的长度.
如图:△ABC是一张直角三角形纸片,其中∠C=90°,BC=8cm,AB=10cm,将纸片折叠,使点A恰好落在BC的中点D处,折痕为MN,试求出AM的长度.