题目内容
7.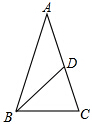 如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由BD是△ABC的角平分线,可得∠ABC=2∠ABD=72°,又可求∠ABC=∠C=72°,所以△ABC是等腰三角形;又∠A=180°-2∠ABC=180°-2×72°=36°,故∠A=∠ABD,所以△ABD是等腰三角形;由∠DBC=∠ABD=36°,得∠C=72°,可求∠BDC=72°,故∠BDC=∠C,所以△BDC是等腰三角形.
解答 解:∵BD是△ABC的角平分线,
∴∠ABC=2∠ABD=72°,
∴∠ABC=∠C=72°,
∴△ABC是等腰三角形…①.
∠A=180°-2∠ABC=180°-2×72°=36°,
∴∠A=∠ABD,
∴△ABD是等腰三角形…②.
∵∠DBC=∠ABD=36°,∠C=72°,
∴∠BDC=72°,
∴∠BDC=∠C,
∴△BDC是等腰三角形…③.
故图中的等腰三角形有3个.
故选C
点评 本题考查了等腰三角形的性质和判定、角的平分线的性质及三角形内角和定理;由已知条件利用相关的性质求得各个角的度数是正确解答本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
13.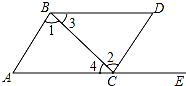 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠D=∠A | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠D=∠DCE |
19.已知y是x的一次函数,表中列出了部分对应值,则m等于-2
| x | -1 | 0 | 1 |
| y | 1 | m | -5 |
16.在△ABC中,∠B=90°,D是AC的中点,若∠A=20°,则∠BDC的度数为( )
| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 如图,在△ABC中,∠C=90°,AC=4,将△ABC沿射线CB方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于8.
如图,在△ABC中,∠C=90°,AC=4,将△ABC沿射线CB方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于8. 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(即:沿着长方形移动一周)
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(即:沿着长方形移动一周)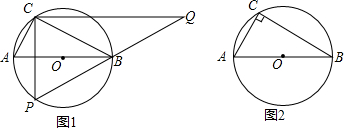 如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.
如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q. 已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.