题目内容
12．二次函数y=-2（x-3）（x+1）的图象与y轴的交点坐标是（0，6）．分析 计算自变量为0时的函数值即可得到抛物线与y轴的交点坐标．
解答 解：当x=0时，y=-2（x-3）（x+1）=6，
所以二次函数y=-2（x-3）（x+1）的图象与y轴的交点坐标为（0，6）．
故答案为：（0，6）．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
相关题目
如图，在矩形纸片ABCD中，CD=12，BC=15，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A1处，求AE的长度．
7．
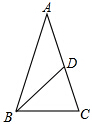如图，在△ABC中，AB=AC，∠A=36°，BD分别是△ABC的角平分线，则图中的等腰三角形共有（ ）
如图，在△ABC中，AB=AC，∠A=36°，BD分别是△ABC的角平分线，则图中的等腰三角形共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．
如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOD=110°，则∠BOD=（ ）
如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOD=110°，则∠BOD=（ ）| A． | 30° | B． | 35° | C． | 20° | D． | 40° |
4．
如图是变量y与x之间的函数图象，则函数y的取值范围是（ ）
如图是变量y与x之间的函数图象，则函数y的取值范围是（ ）| A． | -3≤y≤3 | B． | 0≤y≤2 | C． | 0≤y≤3 | D． | 1≤y≤3 |