题目内容
7.若关于x的方程$\frac{2}{2-x}$+$\frac{2x+m}{x-2}$=1有增根,则m的值是-2.分析 增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母x-2=0,得到x=2,然后代入化为整式方程的方程算出m的值.
解答 解:方程两边都乘(x-2),
得:-2+2x+m=x-2,
∵原方程有增根,
∴最简公分母x-2=0,
解得x=2,
把x=2代入-2+2x+m=x-2得:-2+4+m=2-2,
解得:m=-2.
故答案为:-2.
点评 本题考查了分式方程的增根.增根问题可按如下步骤进行:让最简公分母为0确定增根;化分式方程为整式方程;把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
15.不等式$\frac{x}{3}$>5的解集是( )
| A. | x<$\frac{5}{3}$ | B. | x>$\frac{5}{3}$ | C. | x<15 | D. | x>15 |
12.在圆柱、正方体、长方体中,主视图可能一样的是( )
| A. | 仅圆柱和正方体 | B. | 仅圆柱和长方体 | ||
| C. | 仅正方体和长方体 | D. | 圆柱、正方体和长方体 |
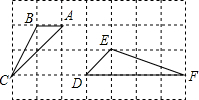 如图,方格纸中每个小正方形的边长都为1,△ABC和△DEF的顶点都在方格纸的格点上.则可判断△ABC和△DEF是否相似:相似(请填“相似”或“不相似”)
如图,方格纸中每个小正方形的边长都为1,△ABC和△DEF的顶点都在方格纸的格点上.则可判断△ABC和△DEF是否相似:相似(请填“相似”或“不相似”) 如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则FC的长为$\frac{5}{3}$.
如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则FC的长为$\frac{5}{3}$.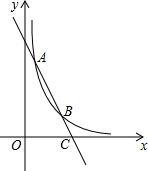 如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).
如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).