题目内容
18.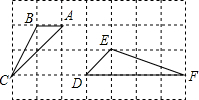 如图,方格纸中每个小正方形的边长都为1,△ABC和△DEF的顶点都在方格纸的格点上.则可判断△ABC和△DEF是否相似:相似(请填“相似”或“不相似”)
如图,方格纸中每个小正方形的边长都为1,△ABC和△DEF的顶点都在方格纸的格点上.则可判断△ABC和△DEF是否相似:相似(请填“相似”或“不相似”)
分析 根据勾股定理求出三角形的各边长,再由相似三角形的判定定理即可得出结论.
解答 解:由图可知,在△ABC中,AB=1,AC=$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$,BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
在△DEF中,DE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,EF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,DF=4,
∵$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{8}}{4}$=$\frac{\sqrt{5}}{\sqrt{10}}$,即$\frac{AB}{DE}$=$\frac{AC}{DF}$=$\frac{BC}{EF}$,
∴△ABC∽△DEF.
故答案为:相似.
点评 本题考查的是相似三角形的判定,熟知三边对应成比例的三角形相似是解答此题的关键.

练习册系列答案
相关题目
6.1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时,2号探测气球从海拔15米处出发,以0.5米/分的速度上升,两个气球都匀速上升了50分钟.
设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由;
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
| 上升时间/分 | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/米 | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/米 | 20 | 30 | … | 0.5x+15 |
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
13.若$\frac{a}{b}=\frac{c}{d}=\frac{1}{2}(b≠d)$,则下列式子不正确的是( )
| A. | $\frac{a+b}{b}=\frac{3}{2}$ | B. | $\frac{a+2c}{b+2d}=2$ | C. | $\frac{a-c}{b-d}=\frac{1}{2}$ | D. | b=2a |
 如图,AB∥CD,∠BAE=135°,∠DCE=40°,则∠AEC=85度.
如图,AB∥CD,∠BAE=135°,∠DCE=40°,则∠AEC=85度.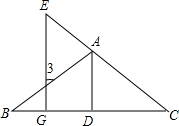 如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.
如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.