题目内容
16.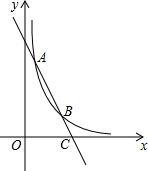 如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).
如图,已知一次函数y=kx+b与反比例函数的图象交于点A(m,6)和B(2,3).(1)求反比例函数的解析式和求一次函数的解析式;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
(3)若直线y=kx+b与x轴交于点C,在x轴上是否存在点D,使得△BCD是以BC为腰的等腰三角形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
分析 (1)利用待定系数法即可求得反比例函数的解析式,则A的坐标即可求得,然后利用待定系数法求得一次函数解析式;
(2)求x在什么范围内时,一次函数的值大于反比例函数的值,就是求一次函数的图象在反比例函数的图象上边的自变量的取值;
(3)首先求得C的坐标,然后分B是顶角顶点和C是顶角顶点两种情况进行讨论,即可求解.
解答 解:(1)设反比例函数的解析式是y=$\frac{k}{x}$,
把B(2,3)代入解析式得:k=6,
则反比例函数的解析式是y=$\frac{6}{x}$.
把(m,6)代入反比例函数的解析式得m=$\frac{6}{6}$=1.
则A的坐标是(1,6).
根据题意得:$\left\{\begin{array}{l}{k+b=6}\\{2k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=9}\end{array}\right.$.
则一次函数的解析式是y=-3x+9;
(2)根据图象可得:当1<x<2时,一次函数的值大于反比例函数的值;
(3)在y=-3x+9中,令y=0,解得:x=3,则C的坐标是(3,0).
作BF⊥x轴于点F,当B时等腰三角形的顶角顶点时,D和C关于F对称,则D的坐标是(1,0);
BC=$\sqrt{(3-2)^{2}+{3}^{2}}$=$\sqrt{10}$,当C是等腰三角形的顶角顶点时,D的坐标是(3+$\sqrt{10}$,0)或($\sqrt{10}$-3,0).
总之,D的坐标是:(1,0)或(3+$\sqrt{10}$,0)或($\sqrt{10}$-3,0).
点评 本题考查了待定系数法求函数的解析式以及等腰三角形的性质,正确对等腰△BCD进行讨论是关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
| 上升时间/分 | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/米 | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/米 | 20 | 30 | … | 0.5x+15 |
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
| A. | a3b3c | B. | a9b3c3 | C. | a3bc3 | D. | a6b3c3 |
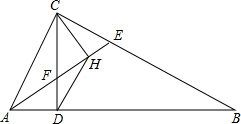 △ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:
△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证: 如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,且点E恰好为DC的中点.求证:BE⊥AE,BE平分∠ABC.
如图,在四边形ABCD中,AD∥BC,AE平分∠BAD交DC于点E,且点E恰好为DC的中点.求证:BE⊥AE,BE平分∠ABC.