题目内容
2. 如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则FC的长为$\frac{5}{3}$.
如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则FC的长为$\frac{5}{3}$.
分析 设CF=x,根据翻折变换的性质用x表示出EF、DF,根据勾股定理求出AE,得到DE的长,根据勾股定理列出方程,解方程即可.
解答 解:设CF=x,
由折叠的性质可知,BE=BC=5,EF=FC=x,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=4,DF=3-x,
∴ED=AD-AE=1,
在Rt△DEF中,EF2=DF2+DE2,即x2=1+(3-x)2,
解得,x=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
12.已知x=3时,分式$\frac{3x+k}{x-1}$的值等于0,则k的值为( )
| A. | 9 | B. | -9 | C. | -3 | D. | 3 |
13.若$\frac{a}{b}=\frac{c}{d}=\frac{1}{2}(b≠d)$,则下列式子不正确的是( )
| A. | $\frac{a+b}{b}=\frac{3}{2}$ | B. | $\frac{a+2c}{b+2d}=2$ | C. | $\frac{a-c}{b-d}=\frac{1}{2}$ | D. | b=2a |
17.若a<b,则下列不等式中错误的是( )
| A. | a+5<b+5 | B. | -4a>-4b | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | a(x2+2)>b(x2+2) |
14.下列计算正确的是( )
| A. | a-(2b-3c)=-(a+2b-3c) | B. | x3-b和-x3-b互为相反数 | ||
| C. | 当x<0时,|3x-x|=-2x | D. | 1×(-1)+2÷(-1)-(-1)=0 |
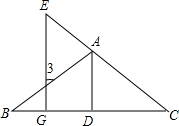 如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.
如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.