题目内容
19.从4点开始,经过$\frac{240}{11}$分钟,时钟的时针和分针在4点至5点之间第一次重合.分析 解决这个问题就要弄清楚时针与分针转动速度的关系:每一小时,分针转动360°,而时针转动30°,即分针每分钟转动6°,时针每分钟转动0.5°,4点时,时针与分针之间的夹角是30°×4=120°,当时钟的时针和分针在4点至5点之间第一次重合时,实际上是分针比时针多走120°,依据这一关系列出方程即可求解.
解答 解:设从4点开始,经过x分钟,时钟的时针和分针在4点至5点之间第一次重合,由题意得:
6x-0.5x=120,
5.5x=120,
x=$\frac{240}{11}$;
即:再经过$\frac{240}{11}$分钟时针和分针第一次重合.
故答案为:$\frac{240}{11}$
点评 本题考查了一元一次方程的应用.钟表上的分钟与时针的转动问题本质上与行程问题中的两人追及问题非常相似,行程问题中的距离相当于这里的角度,行程问题中的速度相当于这里时(分)针的转动速度.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | a-(2b-3c)=-(a+2b-3c) | B. | x3-b和-x3-b互为相反数 | ||
| C. | 当x<0时,|3x-x|=-2x | D. | 1×(-1)+2÷(-1)-(-1)=0 |
4.计算(a2bc)3的结果是( )
| A. | a3b3c | B. | a9b3c3 | C. | a3bc3 | D. | a6b3c3 |
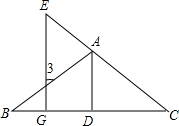 如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.
如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程. 如图,已知a⊥b,b⊥c,c⊥d,求证:a⊥d.
如图,已知a⊥b,b⊥c,c⊥d,求证:a⊥d.