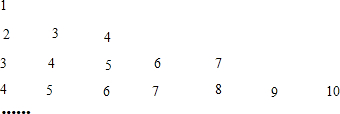题目内容
10．
将足够数量的棱长相等的小正方体摆放成如图的形状，从上往下依次为第一层1个，第二层为1+2=3个，第三层为1+2+3=6个，…，按此规律摆放下去，则第n层（n＞1，n为整数）正方体的个数为$\frac{1}{2}$n（n+1）．
分析 根据题意可以得出从上到下第一层为1，第二层为1+2，…、第n层为：s=1+2+…+n，根据求和公式即可表示．
解答 解：∵第一层有1个正方体，
第二层有1+2=3个；
第三层有1+2+3=6个，
…，
∴第n层有：1+2+3+…+n=$\frac{1}{2}$n（n+1）个，
故答案为：$\frac{1}{2}$n（n+1）．
点评 此题主要考查了图形的变化规律，根据图形得出第n层为：s=1+2+…+n是解决问题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
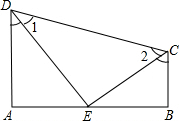如图：已知DA⊥AB，DE平分∠ADC，CE平分∠BCD，且∠1+∠2=90°