��Ŀ����
6����֪a��b��cΪ��ABC������������a2c2-b2c2=a4-b4�����жϡ�ABC����״��С��ͬѧ���������ģ��⣺��a2c2-b2c2=a4-b4����c2��a2-b2��=��a2+b2����a2-b2��
��$\frac{{c}^{2}={a}^{2}+{b}^{2}}{��}$�� ���������ABC��ֱ�������Σ�
�������ʺ�����ʦ��������ע����ʦ��д�������������Ľ���˼·������������������г����˴�����������˼��һ�£�һ����д�������Ľ�����̣����������С���������⣬����
���� ���ݹ۲��֪������ֻ��c2=a2+b2����a2-b2=0���Ͳ���ó�c2=a2+b2����a2-b2��0���ɵó�c2=a2+b2����Ȼ��������������ۣ�
��� �⣺��a2c2-b2c2=a4-b4����c2��a2-b2��=��a2+b2����a2-b2��
��c2��a2-b2��-��a2-b2����a2+b2��=0��
�ࣨa2-b2��[c2-��a2+b2��]=0��
��a2-b2=0��c2-��a2+b2��=0����a=b��c2=a2+b2��
���ABC�ǵ��������λ�ֱ�������λ����ֱ��������
���� ���⿼�鹴�ɶ������涨����Ӧ�á��������ۣ��ж��������Ƿ�Ϊֱ�������Σ���֪���������ߵij���ֻҪ���ù��ɶ������涨�������жϼ��ɣ�

��ϰ��ϵ�д�
�����Ŀ
18��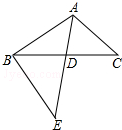 ��ͼ����ABC�У�AE��BC�ڵ�D����C=��CBE��AD��DE=3��5��BD=4����DC�ij����ڣ�������
��ͼ����ABC�У�AE��BC�ڵ�D����C=��CBE��AD��DE=3��5��BD=4����DC�ij����ڣ�������
 ��ͼ����ABC�У�AE��BC�ڵ�D����C=��CBE��AD��DE=3��5��BD=4����DC�ij����ڣ�������
��ͼ����ABC�У�AE��BC�ڵ�D����C=��CBE��AD��DE=3��5��BD=4����DC�ij����ڣ�������| A�� | $\frac{15}{4}$ | B�� | $\frac{12}{5}$ | C�� | $\frac{20}{3}$ | D�� | $\frac{17}{4}$ |
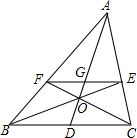 ��ͼ����֪��ABC����E�ڱ�AC�ϣ���F�ڱ�AB�ϣ�EF��BC��BE��CF���ڵ�O������AO��EF�ڵ�G���ӳ�AO��BC�ڵ�D����֤��BD=CD��EG=FG��
��ͼ����֪��ABC����E�ڱ�AC�ϣ���F�ڱ�AB�ϣ�EF��BC��BE��CF���ڵ�O������AO��EF�ڵ�G���ӳ�AO��BC�ڵ�D����֤��BD=CD��EG=FG��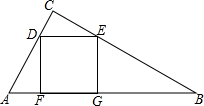 ��ͼ����֪��ABC�У��ı���DEGFΪ�����Σ�D��E���߶�AC��BC�ϣ�F��G��AB�ϣ����S��ADF=S��CDE=1��S��BEG=3�����ABC�������
��ͼ����֪��ABC�У��ı���DEGFΪ�����Σ�D��E���߶�AC��BC�ϣ�F��G��AB�ϣ����S��ADF=S��CDE=1��S��BEG=3�����ABC������� ������ֵ��3��x2-2xy��-[��-$\frac{1}{2}$xy+y2��+��x2-2y2��]������x��y��ֵ�������ʾ��
������ֵ��3��x2-2xy��-[��-$\frac{1}{2}$xy+y2��+��x2-2y2��]������x��y��ֵ�������ʾ�� ��ͼ��ʾ��E�ǡ�AOB��ƽ������һ�㣬EC��OA��ED��OB������ֱ�Ϊ��C��D����֤��
��ͼ��ʾ��E�ǡ�AOB��ƽ������һ�㣬EC��OA��ED��OB������ֱ�Ϊ��C��D����֤��