题目内容
18.有一组按规律排列的单项式:-x,$\frac{{x}^{2}}{2}$,-$\frac{{x}^{3}}{3}$,$\frac{{x}^{4}}{4}$,….(1)它们的规律是什么?
(2)写出第100个,第2011个单项式.
(3)写出第2n个,第2n+1个单项式.
分析 (1)观察分子、分母以及分式本身的符号来寻找规律;
(2)(3)根据(1)中的规律解题.
解答 解:(1)-x=(-1)1•$\frac{{x}^{1}}{1}$,
$\frac{{x}^{2}}{2}$=(-1)2•$\frac{{x}^{2}}{2}$,
-$\frac{{x}^{3}}{3}$=(-1)3•$\frac{{x}^{3}}{3}$,
$\frac{{x}^{4}}{4}$=(-1)4•$\frac{{x}^{4}}{4}$,
…
第n个单项式为:(-1)n•$\frac{{x}^{n}}{n}$;
(2)由(1)知,第n个单项式为:(-1)n•$\frac{{x}^{n}}{n}$.
则第100个单项式:(-1)100•$\frac{{x}^{100}}{100}$=$\frac{{x}^{100}}{100}$.
第2011个单项式:(-1)2011•$\frac{{x}^{2011}}{2011}$=-$\frac{{x}^{2011}}{2011}$.
(3)第2n个单项式:(-1)2n•$\frac{{x}^{2n}}{2n}$=$\frac{{x}^{2n}}{2n}$.
第2011个单项式:(-1)(2n+1)•$\frac{{x}^{2n+1}}{2n+1}$=-$\frac{{x}^{2n+1}}{2n+1}$.
点评 本题考查了单项式.根据所给的单项式找到规律是解题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若(m-1)2+$\sqrt{n+2}$=0,则nm的值是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
 如图,将一块长50厘米、宽40厘米的铁皮剪去四个正方形的角,就可以折成一个长方体无盖盒子.如果盒子的底面积为600平方厘米,求盒子的高度.
如图,将一块长50厘米、宽40厘米的铁皮剪去四个正方形的角,就可以折成一个长方体无盖盒子.如果盒子的底面积为600平方厘米,求盒子的高度.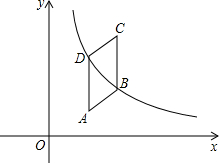 如图,在?ABCD中,AB⊥BD,sinA=$\frac{4}{5}$,将?ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=$\frac{k}{x}$(k>0)同时经过B、D两点,则点B的坐标是($\frac{9}{5}$,$\frac{4}{3}$).
如图,在?ABCD中,AB⊥BD,sinA=$\frac{4}{5}$,将?ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=$\frac{k}{x}$(k>0)同时经过B、D两点,则点B的坐标是($\frac{9}{5}$,$\frac{4}{3}$).