题目内容
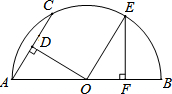 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为( )| A、8 | B、7 | C、6 | D、4 |
考点:垂径定理,全等三角形的判定与性质
专题:
分析:先根据垂径定理求出AD的长,再由AAS定理得出△ADO≌△OFE,推出OF=AD即可求出答案.
解答:解:∵OD⊥AC,AC=12,
∴AD=CD=6,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中,
∵
,
∴△ADO≌△OFE(AAS),
∴OF=AD=6,
故选C.
∴AD=CD=6,
∵OD⊥AC,EF⊥AB,
∴∠ADO=∠OFE=90°,
∵OE∥AC,
∴∠DOE=∠ADO=90°,
∴∠DAO+∠DOA=90°,∠DOA+∠EF=90°,
∴∠DAO=∠EOF,
在△ADO和△OFE中,
∵
|
∴△ADO≌△OFE(AAS),
∴OF=AD=6,
故选C.
点评:本题的是垂径定理,全等三角形的性质和判定等知识,解此题的关键是求出△ADO≌△OFE和求出AD的长,注意:垂直于弦的直径平分这条弦.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
若抛物线y=(1+m)xm2-2的开口向下,则m的值为( )
| A、2 | B、-2 | C、±2 | D、1 |
 如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )| A、120° | B、100° |
| C、80° | D、60° |
下面判断正确的是( )
| A、一个数的相反数不是负数,这个数一定是负数 |
| B、一个数的绝对值是正数,这个数一定是正数 |
| C、两个数的和是正数,这两个数一定都是正数 |
| D、两个数的乘积为1,这两个数一定互为倒数 |
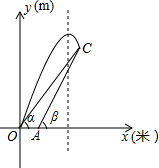 如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tan
如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tan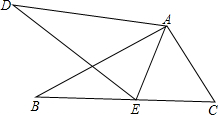 如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件