题目内容
 如图,?ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,求?ABCD的面积.
如图,?ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,求?ABCD的面积.考点:平行四边形的性质
专题:
分析:过点A作AE⊥BD于E,设OE=a,则AE=
a,OA=2a,在直角三角形ADE中,利用勾股定理可得DE2+AE2=AD2,进而可求出a的值,△ABD的面积可求出,由平行四边形的性质可知:?ABCD的面积=2S△ABD,问题得解.
| 3 |
解答:解:∵四边形ABCD是平行四边形,
∴OD=
BD=
×10=5,
∵∠BOC=120°,
∴∠AOE=60°,
设OE=a,则AE=
a,OA=2a,
∴DE=5+a,
在直角三角形ADE中,由勾股定理可得DE2+AE2=AD2,
∴(5+a)2+(
a)2=72,
解得:a=
,
∴AE=
×
=
,
∴?ABCD的面积=2S△ABD=
.
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BOC=120°,
∴∠AOE=60°,

设OE=a,则AE=
| 3 |
∴DE=5+a,
在直角三角形ADE中,由勾股定理可得DE2+AE2=AD2,
∴(5+a)2+(
| 3 |
解得:a=
| 3 |
| 8 |
∴AE=
| 3 |
| 3 |
| 8 |
3
| ||
| 8 |
∴?ABCD的面积=2S△ABD=
15
| ||
| 4 |
点评:此题考查了平行四边形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
下列说法不正确的是( )
A、
| ||||||
| B、全体实数与数轴上的点一一对应 | ||||||
C、当x<0时,
| ||||||
D、
|
在下列命题中,正确的是( )
| A、三点确定一个圆 |
| B、圆的内接等边三角形只有一个 |
| C、一个三角形有且只有一个外接圆 |
| D、一个四边形一定有外接圆 |
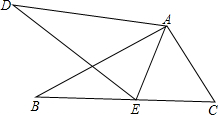 如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件