题目内容
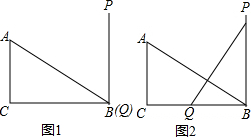 如图,在△ABC中,∠ACB=90°,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于
如图,在△ABC中,∠ACB=90°,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于考点:全等三角形的判定
专题:动点型,分类讨论
分析:分情况进行讨论:①当Q与C重合时,AC=BP=3时,△BCA≌△QBP;②当BP=BC=4时,△BCA≌△PBQ.
解答:解:①当Q与C重合时,AC=BP=3时,△BCA≌△QBP,
在Rt△BCA和Rt△QBP中,
,
∴Rt△BCA≌Rt△QBP(HL);
②当BP=BC=4时,△BCA≌△PBQ,
在Rt△BCA和Rt△QAC中,
,
∴Rt△BCA≌Rt△PBQ(HL).
故答案为:4或3.
在Rt△BCA和Rt△QBP中,
|
∴Rt△BCA≌Rt△QBP(HL);
②当BP=BC=4时,△BCA≌△PBQ,
在Rt△BCA和Rt△QAC中,
|
∴Rt△BCA≌Rt△PBQ(HL).
故答案为:4或3.
点评:本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关健.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
=
,则
的值等于( )
| a |
| b |
| 4 |
| 3 |
| a+b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
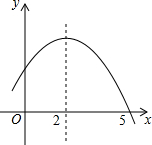 二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )
二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )| A、x1=-1,x2=5 |
| B、x1=-2,x2=4 |
| C、x1=-1,x2=2 |
| D、x1=-5,x2=5 |
 如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )| A、120° | B、100° |
| C、80° | D、60° |
下列说法不正确的是( )
A、
| ||||||
| B、全体实数与数轴上的点一一对应 | ||||||
C、当x<0时,
| ||||||
D、
|
 如图,已知△ABC中,∠C=90°,∠A=60°,a=15,根据定义求∠A,∠B的三角函数值.
如图,已知△ABC中,∠C=90°,∠A=60°,a=15,根据定义求∠A,∠B的三角函数值.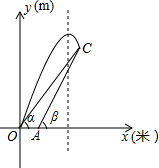 如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tan
如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tan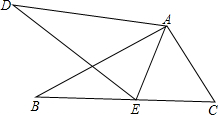 如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件