题目内容
18．
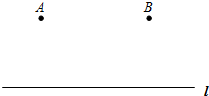如图：A村和B村在公路l同侧，且AB=3千米，两村距离公路都是2千米．现决定在公路l上建立一个供水站P，要求使PA+PB最短．（1）用尺规作图，作出点P； （作图要求：不写作法，保留作图痕迹）
（2）求出PA+PB的最小值．
分析 （1）首先作出A点的对称点A′，然后连接BA′，找到交点P点；
（2）首先连接AB，由题意知AB=3km，A A′=4km，然后由勾股定理求得A′B的长，即PA+PB的最小值．
解答 
解：（1）作图，如右图，
作出A点的对称点A′，
连接BA′，找到交点P点；
（2）连接AB，由题意知AB=3km，A A′=4km，
在Rt△A A′B中，根据勾股定理得：A′B2=42+32，
∴A′B=5km，
即PA+PB=A′B=5km，
答：PA+PB的最小值是5km．
点评 此题考查了最短路径问题以及勾股定理．注意准确找到点P是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC中，∠ACB=90°，CD是高，若∠A=30°，BD=1，则BC=2，AD=3．
9．-$\frac{1}{6}$的相反数是（ ）
| A． | -6 | B． | -$\frac{1}{6}$ | C． | $\frac{1}{6}$ | D． | 6 |
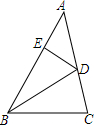如图，BD是△ABC的角平分线，DE⊥AB，垂足为E，△ABC的面积为70，AB=16，BC=12，则DE的长为5．
13．已知a+2与2a-5都是m的平方根，则m的值是（ ）
| A． | 1 | B． | 9 | C． | -3 | D． | 3 |
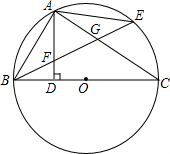如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，AE=AB，BE分别交AD、AC于点F、G．
7．方程2（x-3）2=8的根是（ ）
| A． | x1=2，x2=-2 | B． | x1=5，x2=1 | C． | x1=-5，x2=-1 | D． | x1=-5，x2=-1 |