题目内容
6.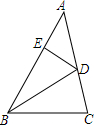 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,△ABC的面积为70,AB=16,BC=12,则DE的长为5.
如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,△ABC的面积为70,AB=16,BC=12,则DE的长为5.
分析 作DF⊥BC于F,根据角平分线的性质得到DF=DE,根据三角形面积公式计算即可.
解答  解:作DF⊥BC于F,
解:作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE,
∴$\frac{1}{2}$×AB×DE+$\frac{1}{2}$×BC×DF=70,
∴DF=DE=5.
故答案为:5.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.如果x=y,a为有理数,那么下列等式不一定成立的是( )
| A. | 1-y=1-x | B. | x2=y2 | C. | $\frac{x}{a}$=$\frac{y}{a}$ | D. | ax=ay |
11.等腰三角形的周长是16,一边长为4,则这个等腰三角形腰长为( )
| A. | 4 | B. | 6 | C. | 4或6 | D. | 8 |
15.方程x2=2x的解是( )
| A. | x=2 | B. | x=0 | C. | x1=2,x2=0 | D. | x1=$\sqrt{2}$,x2=0 |

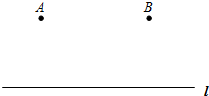 如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短.
如图:A村和B村在公路l同侧,且AB=3千米,两村距离公路都是2千米.现决定在公路l上建立一个供水站P,要求使PA+PB最短. 如图是一个三级台阶,它的每一级的长、宽和高分别为5dm、3dm和1dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是13dm.
如图是一个三级台阶,它的每一级的长、宽和高分别为5dm、3dm和1dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是13dm.