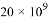题目内容
8.先化简,再求值:(x+1-$\frac{3x}{{x}^{2}-x}$)÷($\frac{{x}^{2}}{x-1}$-4),其中x=$\sqrt{2}$+2.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=[x+1-$\frac{3x}{x-1}$]÷[$\frac{{x}^{2}}{x-1}$-$\frac{4(x-1)}{x-1}$]
=$\frac{{x}^{2}-4}{x-1}$÷$\frac{(x-2)^{2}}{x-1}$
=$\frac{(x+2)(x-2)}{x-1}$•$\frac{x-1}{{(x-2)}^{2}}$
=$\frac{x+2}{x-2}$,
当x=$\sqrt{2}$+2时,原式=$\frac{\sqrt{2}+4+2}{\sqrt{2}+2-2}$=1+2$\sqrt{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
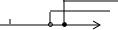
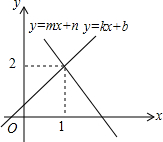 如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.

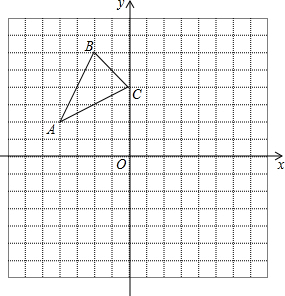 如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.
如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点. 如图点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,∠A=43°.
如图点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,∠A=43°.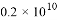 B.
B. 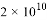 C.
C.  D.
D.