题目内容
11．
如图，四边形ABCD内接于⊙O，AB=AD，∠C=110°，点E在$\widehat{AD}$上，则∠E=125°．
分析 先根据圆内接四边形的性质得∠BAD=180°-∠C=70°，则利用等腰三角形的性质和三角形内角和定理计算出∠ABD=∠ADB=$\frac{1}{2}$（180°-∠BAD）=55°，然后再根据圆内接四边形的性质求∠E的度数．
解答 解：∵∠BAD+∠C=180°，
而∠C=110°，
∴∠BAD=180°-110°=70°，
∵AB=AD，
∴∠ABD=∠ADB=$\frac{1}{2}$（180°-∠BAD）=$\frac{1}{2}$（180°-70°）=55°，
∵∠ABD+∠E=180°，
∴∠E=180°-55°=125°．
故答案为125．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了圆内接四边形的性质．
练习册系列答案
阅读快车系列答案
相关题目
1．
如图，已知AB∥CD，CE交AB于点F，若∠E=20°，∠C=45°，则∠A的度数为（ ）
如图，已知AB∥CD，CE交AB于点F，若∠E=20°，∠C=45°，则∠A的度数为（ ）| A． | 5° | B． | 15° | C． | 25° | D． | 35° |
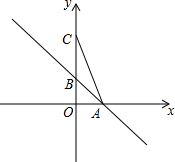如图，一次函数y=-x+1的图象与x轴、y轴分别交于点A、B．点C在y轴的正半轴上，且sin∠ACB=$\frac{\sqrt{10}}{10}$ 
如图，射线AB，CD分别与直线l相交于点G、H，若∠1=∠2，∠C=65°，则∠A的度数是115°．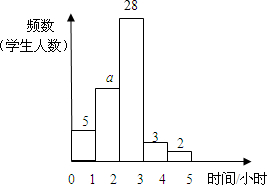
某中学九年级（1）班50名学生参加平均每周上网时间的调查，由调查结果绘制了频数分布直方图，根据图中信息回答下列问题：
如图，过反比例函数y=$\frac{k}{x}$图象上三点A、B、C分别作直角三角形和矩形，图中S1+S2=5，则S3=5．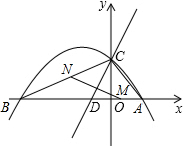
已知抛物线y=ax2+bx+c（a＜0）与x轴交于点A（8，0）和B（-12，0），与y轴交于点C（0，6）．
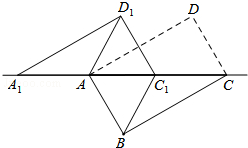如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连结AD1、BC1．若∠ACB=30°，AB=1，CC1=x，△ACD与△A1C1D1重叠部分的面积为s，则下列结论：