题目内容
等腰△ABC中,AB=AC,△ABC的周长为20,且有(BC+1)2=AB,则△ABC的腰长和底边长分别是 .
考点:一元二次方程的应用
专题:几何图形问题
分析:可设△ABC的腰长为x,则底边长为20-2x,根据(BC+1)2=AB,列出方程求解即可.
解答:解:设△ABC的腰长为x,则底边长为20-2x,依题意有
(20-2x+1)2=x,
解得x1=
(舍去),x2=9,
20-2x=20-18=2.
答:△ABC的腰长和底边长分别是9和2.
故答案为:9和2.
(20-2x+1)2=x,
解得x1=
| 49 |
| 4 |
20-2x=20-18=2.
答:△ABC的腰长和底边长分别是9和2.
故答案为:9和2.
点评:考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
下列图形中对称轴最多的是( )
| A、圆 | B、正方形 |
| C、等边三角形 | D、线段 |
 如图,将三条线段CD,EF,GN分别绕点O旋转,不能与线段AB重合的线段是
如图,将三条线段CD,EF,GN分别绕点O旋转,不能与线段AB重合的线段是
 如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.
如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.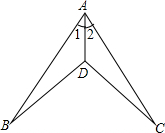 如图,∠1=∠2,由SAS判定△ABD≌△ACD,则需添加的条件
如图,∠1=∠2,由SAS判定△ABD≌△ACD,则需添加的条件 已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,还要添加的条件为
已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,还要添加的条件为 如图,ABCD是一个长方形盒子的正面,小明想知道AB边与CD边是否垂直于BC边,他利用随身带的卷尺量得AB=5cm,BC=12cm,A、C两点的距离是13cm.由此,小明判断出AB边垂直于BC边.你知道这是为什么吗?
如图,ABCD是一个长方形盒子的正面,小明想知道AB边与CD边是否垂直于BC边,他利用随身带的卷尺量得AB=5cm,BC=12cm,A、C两点的距离是13cm.由此,小明判断出AB边垂直于BC边.你知道这是为什么吗?