题目内容
13.如果方程组$\left\{\begin{array}{l}{x+2y=5}\\{2x+4y=k}\end{array}\right.$有无穷多解,那么方程组$\left\{\begin{array}{l}{kx+2y=7}\\{5x+4y=8}\end{array}\right.$的解的情况有( )| A. | 唯一有解 | B. | 无穷多解 | C. | 无解 | D. | 都有可能 |
分析 由已知关于x、y的方程组$\left\{\begin{array}{l}{x+2y=5}\\{2x+4y=k}\end{array}\right.$有无穷多组解,则直线x+2y=5与直线2x+4y=k重合,根据两条直线重合对应系数成比例,构造关于k的方程,解方程即可得到答案.
解答 解:因为已知关于x、y的方程组$\left\{\begin{array}{l}{x+2y=5}\\{2x+4y=k}\end{array}\right.$有无穷多组解,
所以可得直线x+2y=5与直线2x+4y=k重合,
可得:k=10,
把k=10代入方程组$\left\{\begin{array}{l}{kx+2y=7}\\{5x+4y=8}\end{array}\right.$中,可得:$\left\{\begin{array}{l}{10x+2y=7}\\{5x+4y=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=\frac{3}{2}}\end{array}\right.$,
故选A
点评 本题考查的知识点是直线的一般式方程与直线的平行关系,其中根据已知分析出两条直线重合是解答本题的关键.

练习册系列答案
相关题目
1.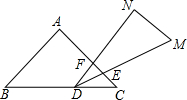 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E,F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是( )| A. | 105° | B. | 115° | C. | 120° | D. | 135° |
3.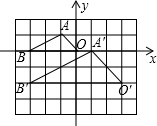 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )| A. | (0,0) | B. | (0,1) | C. | (-3,2) | D. | (3,-2) |
 十字交叉线
十字交叉线