题目内容
3.化简:$\frac{\sqrt{xy}}{y\sqrt{x}-x\sqrt{y}}$(x>0,y>0)分析 先利用分母有理化进行化简即可.
解答 解:因为x>0,y>0,
所以$\frac{\sqrt{xy}}{y\sqrt{x}-x\sqrt{y}}$
=$\frac{\sqrt{xy}(y\sqrt{x}+x\sqrt{y})}{(y\sqrt{x}-x\sqrt{y})(y\sqrt{x}+x\sqrt{y})}$
=$\frac{xy\sqrt{y}+xy\sqrt{x}}{{y}^{2}x-{x}^{2}y}$
=$\frac{\sqrt{y}+\sqrt{x}}{y-x}$.
点评 此题考查二次根式的化简,关键是根据分母有理化进行计算.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.计算:$\sqrt{17}÷\sqrt{85}•\sqrt{5}$=( )
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
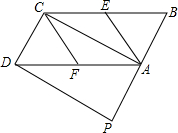 如图,在?ABCD中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DP∥AC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.
如图,在?ABCD中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DP∥AC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.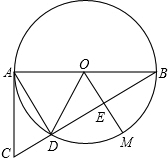 如图,⊙O是△ABD的外接圆,AB是⊙O的直径,M为⊙O上一点,OM⊥BC,垂足为E,点C在BD的延长线上,连接CA,∠CAD=∠CBA
如图,⊙O是△ABD的外接圆,AB是⊙O的直径,M为⊙O上一点,OM⊥BC,垂足为E,点C在BD的延长线上,连接CA,∠CAD=∠CBA 如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.
如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.