题目内容
18.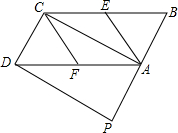 如图,在?ABCD中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DP∥AC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.
如图,在?ABCD中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DP∥AC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.
分析 首先根据平行四边形的性质可得CB∥AD,CB=AD.AB∥CD,再根据中点定义可得CE=AF,进而可证明四边形AFCE是平行四边形,然后再证明四边形CDPA是矩形,可得∠DCA=90°,再根据直角三角形的性质可证明CF=AF,进而可证出四边形AECF是菱形.
解答 证明:∵四边形ABCD是平行四边形,
∴CB∥AD,CB=AD.AB∥CD,
∵E、F分别是边BC,AD的中点,
∴CE=$\frac{1}{2}$CB,AF=$\frac{1}{2}$AD.
∴CE=AF,
∴四边形AFCE是平行四边形,
∵∠P=90°,AB∥CD, CB∥AD,
CB∥AD,
∴四边形CDPA是矩形,
∴∠ACD=90°,
在Rt△ADB中
∵F为AB的中点,
∴AF=CF=DF,
∵四边形CFAE是平行四边形,
∴四边形CFAE是菱形.
点评 本题主要考查了平行四边形的性质、菱形的判定,直角三角形的性质,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知在△ABC中,∠B=60°,∠C=90°,CE、AD分别为∠C、∠A的角平分线,求证:EF=FD.
已知在△ABC中,∠B=60°,∠C=90°,CE、AD分别为∠C、∠A的角平分线,求证:EF=FD.
 如图,在△ABC中,AB=6,AC=8,∠CAB=60°.求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.
如图,在△ABC中,AB=6,AC=8,∠CAB=60°.求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.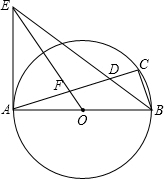 如图,AB为⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E,连接OE交AC于F.
如图,AB为⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E,连接OE交AC于F. 如图,直线AB、CD交于O,∠BOE=∠COF=90°,∠EOF=140°,求∠AOD的度数.
如图,直线AB、CD交于O,∠BOE=∠COF=90°,∠EOF=140°,求∠AOD的度数.