��Ŀ����
3�� ��ͼ����A��������C1��y=$\frac{1}{2}$x2+2x+1�Ķ��㣬��B��������C2��y=$\frac{1}{2}$x2+bx+c�Ķ��㣬����OB��OA��
��ͼ����A��������C1��y=$\frac{1}{2}$x2+2x+1�Ķ��㣬��B��������C2��y=$\frac{1}{2}$x2+bx+c�Ķ��㣬����OB��OA����1�����A�����ꣻ
��2����OB=2$\sqrt{5}$����������C2�ĺ�������ʽ��
��3���ڣ�2�������£���PΪx���ϵ�һ�����㣬̽������������C1��C2���Ƿ���ڵ�Q��ʹ�Ե�O��B��P��QΪ������ı�����ƽ���ı��Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���� ��1������Ϊ����ʽ���ɵõ���A�����ꣻ
��2����AD��x���ڵ�D��BC��x�ڵ�C����֤����AOD�ס�OBC���������������ζ�Ӧ�߳ɱ������BC��OC�ij����õ�B��������ɶ���ʽ���������C2�ĺ�������ʽ��
��3����Q��m��n�������ı���QPBO��ƽ���ı��Σ���n=4��Ȼ�����������C1��C2�Ͻⷽ�̼������m��ֵ���õ���Q�����꣮
��� �⣺��1����y=$\frac{1}{2}$x2+2x+1=$\frac{1}{2}$��x+2��2-1��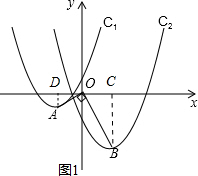
�ඥ��A��-2��-1��
��2����ͼ1����AD��x���ڵ�D��BC��x�ڵ�C��
�ɣ�1����AD=1��OD=2��OA=$\sqrt{5}$
��AD��x�ᣬBC��x�ᣬ
���ADO=��OCB=90�㣬
��OB��OA��
���AOD=��OBC��
���AOD�ס�OBC��
��$\frac{BC}{OD}=\frac{OB}{OA}$����$\frac{BC}{2}=\frac{2\sqrt{5}}{\sqrt{5}}$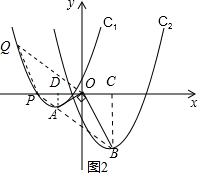
��BC=4��ͬ���ɵ�OC=2��
��B��2��-4����
��������C2��y=$\frac{1}{2}$��x-2��2-4��
��y=$\frac{1}{2}$x2-2x-2��
��3����Q��m��n������ͼ2����ƽ���ı���QPBO�У�
���ڶԽ���ƽ��ƽ���ı��Σ�
��n=4���ɵ�$\frac{1}{2}$m2+2m+1=4��$\frac{1}{2}$m2-2m-2=4��
��m=-2��$\sqrt{10}$��-2��6��
��m=-2ʱ��Q��O��B���㹲�ߣ����������������
��Q1��-2-$\sqrt{10}$��4����Q2��-2+$\sqrt{10}$��4����Q3��6��4����
���� ������Ҫ�����˶��κ������ۺ����ã����������������ε��ж������ʡ�ƽ���ı��ε��ж��������Լ����ɶ�������κ���������⣬���н�ǿ�����ν�������ǽ������Ĺؼ���

 ��ͼ��AB�ǡ�O��ֱ����AF�ǡ�O�����ߣ���CD��AB��E��CF��DA��DE=2$\sqrt{3}$��AO-OE=2��֤���ı���AFCD�����Σ������O��FC�ľ��룮
��ͼ��AB�ǡ�O��ֱ����AF�ǡ�O�����ߣ���CD��AB��E��CF��DA��DE=2$\sqrt{3}$��AO-OE=2��֤���ı���AFCD�����Σ������O��FC�ľ��룮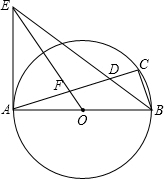 ��ͼ��ABΪ��O��ֱ������C�ڡ�O�ϣ���ABC��ƽ������AC�ཻ�ڵ�D�����O����A�������ཻ�ڵ�E������OE��AC��F��
��ͼ��ABΪ��O��ֱ������C�ڡ�O�ϣ���ABC��ƽ������AC�ཻ�ڵ�D�����O����A�������ཻ�ڵ�E������OE��AC��F�� ����Ӱ���ֵ������
����Ӱ���ֵ������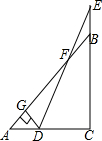 ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=2����D���߶�AC�ϵĵ㣬��E���߶�CB�ӳ����ϵĵ㣬��BE=AD������DE��AB�ڵ�F������D��DG��AB������ΪG�����߶�FG�ij�Ϊ$\sqrt{2}$��
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=2����D���߶�AC�ϵĵ㣬��E���߶�CB�ӳ����ϵĵ㣬��BE=AD������DE��AB�ڵ�F������D��DG��AB������ΪG�����߶�FG�ij�Ϊ$\sqrt{2}$��