题目内容
6.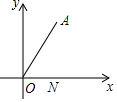 如图,点A(2,2$\sqrt{3}$),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为$\frac{3}{2}$.
如图,点A(2,2$\sqrt{3}$),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为$\frac{3}{2}$.
分析 MO=MA知点P在AO中垂线上,当MN⊥PQ时MN最小,利用△PMN∽△PQO得$\frac{PN}{PO}$=$\frac{MN}{QO}$,据此求解可得.
解答 解:如图,过点A作AB⊥x轴,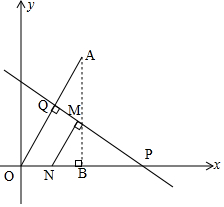
则OB=2、AB=2$\sqrt{3}$,
∴OA=$\sqrt{O{B}^{2}+A{B}^{2}}$=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4,
∵cos∠AOB=$\frac{OB}{OA}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠AOB=60°,
作AO的中垂线交x轴于点P,交OA于点Q,
则OQ=AQ=2,
∴OP=$\frac{OQ}{cos∠AOB}$=4,
∵N(1,0),
∴PN=3,
∵MO=MA,
∴点M在PQ上,
当MN⊥PQ时,MN最小,
∵PQ⊥OA、PQ⊥MN,
∴△PMN∽△PQO,
∴$\frac{PN}{PO}$=$\frac{MN}{QO}$,即$\frac{3}{4}$=$\frac{MN}{2}$,
解得:MN=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题主要考查线段垂直平分线的性质、相似三角形的判定与性质及解直角三角形的应用,熟练掌握中垂线的性质得出点M的位置时解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.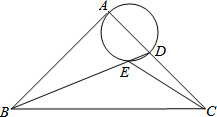 如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )
如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )
 如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )
如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )| A. | 2 | B. | 4 | C. | $2\sqrt{2}-2$ | D. | $2\sqrt{5}-2$ |
18.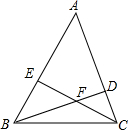 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )| A. | 20$\sqrt{3}$ | B. | 25$\sqrt{3}$ | C. | 30$\sqrt{3}$ | D. | 40$\sqrt{3}$ |
16.2016年10月28日,随着深圳地铁7,9号线的相继开通,深圳地铁日均客流量达到470万人次,则470万用科学记数法表示为( )
| A. | 47×104 | B. | 47×105 | C. | 4.7×105 | D. | 4.7×106 |
 如图所示,在每个边长都为1的小正方形组成的网格中,点A、B、C均为格点.
如图所示,在每个边长都为1的小正方形组成的网格中,点A、B、C均为格点. 如图,在平面直角坐标系xOy中,抛物线y=$\frac{1}{4}$x2+bx+c经过点A(-2,0)和原点,点B在抛物线上且tan∠BAO=$\frac{1}{2}$,抛物线的对称轴与x轴相交于点P.
如图,在平面直角坐标系xOy中,抛物线y=$\frac{1}{4}$x2+bx+c经过点A(-2,0)和原点,点B在抛物线上且tan∠BAO=$\frac{1}{2}$,抛物线的对称轴与x轴相交于点P. 如图,在△ABC中,∠BAC=90°,AB=AC,点O是BC中点,点D、E分别在BA、AC的延长线上,且OD⊥OE,说明OD=OE.
如图,在△ABC中,∠BAC=90°,AB=AC,点O是BC中点,点D、E分别在BA、AC的延长线上,且OD⊥OE,说明OD=OE. 如图:证明:∠A+∠B+∠C=180°.
如图:证明:∠A+∠B+∠C=180°.