题目内容
10.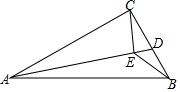 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是$\sqrt{61}$-6cm.
如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是$\sqrt{61}$-6cm.
分析 由∠AEC=90°知E在以AC为直径的⊙M的$\widehat{CN}$上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC,根据相似三角形的性质得到MF,根据勾股定理得到AF,BF,BM,于是得到结论.
解答 解:如图,
由题意知,∠AEC=90°,
∴E在以AC为直径的⊙M的$\widehat{CN}$上(不含点C、可含点N),
∴BE最短时,即为连接BM与⊙M的交点(图中点E′点),
∵AB=13cm,AC=12cm,BC=5cm,
∴AC2+BC2=AB2,
∴∠ACB=90°,
作MF⊥AB于F,
∴∠AFM=∠ACB=90°,∠FAM=∠CAB,
∴△AMF∽△ABC,
∴$\frac{MF}{BC}$=$\frac{AM}{AB}$,即$\frac{MF}{5}$=$\frac{6}{13}$,得MF=$\frac{30}{13}$,
∴AF=$\sqrt{A{M}^{2}-M{F}^{2}}$=$\frac{72}{13}$,
则BF=AB-AF=$\frac{97}{13}$,
∴BM=$\sqrt{M{F}^{2}+B{F}^{2}}$=$\sqrt{61}$,
∵ME=6,
∴BE长度的最小值BE′=BM-ME′=$\sqrt{61}$-6,
故答案为:$\sqrt{61}$-6.
点评 本题主要考查圆周角定理、勾股定理、相似三角形的判定与性质等知识点,根据题意得出BE最短时,即为连接BM与⊙M的交点是解题的关键.

练习册系列答案
相关题目
1.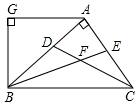 如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
①∠BAG=2∠ABE;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.
其中正确的结论是( )
 如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABE;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.
其中正确的结论是( )
| A. | ①③④ | B. | ②④ | C. | ①③ | D. | ①②③④ |
5.下列说法错误的是( )
| A. | 4的算术平方根是2 | B. | 16的平方根是±4 | ||
| C. | 5是25的平方根 | D. | (-6)2的平方根是-6 |
15.一组数据的方差为s2,将这组数据中的每一个数据都扩大到原来的3倍,所得的一组新数的方差是( )
| A. | $\frac{{s}^{2}}{9}$ | B. | 9s2 | C. | 3s2 | D. | s2 |
2.$\sqrt{4}$的值是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | ±4 |
19.若(m-n)(m-n-2)-8=0,则m-n的值为( )
| A. | 4或-2 | B. | 4 | C. | -2 | D. | 2 |