题目内容
如图，CD是Rt△ABC斜边AB边上的高，AB=10cm，BC=8cm，则CD的长为（ ）| A、6cm | B、4.8cm |
| C、2.4cm | D、1.2cm |
考点：勾股定理
专题：
分析：在Rt△ABC中，由勾股定理可求出直角边AC的长，进而可根据直角三角形面积的不同表示方法求出CD的长．
解答：解：在Rt△ABC中，∠ACB=90°，AB=10cm，BC=8cm，
由勾股定理得：AC=
=
=6（cm）．
而△ABC的面积S=
AC•BC=
AB•CD，
∴CD=
=4.8（cm）．
故选：B．
由勾股定理得：AC=
| AB2-BC2 |
| 102-82 |
而△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
故选：B．
点评：此题主要考查了勾股定理和直角三角形面积的不同表示方法，解题关键是首先根据勾股定理求出AC的长，难度一般．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
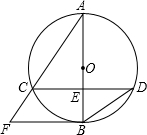如图，已知⊙O的直径AB与弦CD互相垂直，垂足为E．⊙O的切线BF与弦AC的延长线相交于点F，且AC=8，tan∠BDC=
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列四个结论中：