题目内容
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列四个结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列四个结论中:①2a-b<0;②abc<0;③a+b+c<0;④a-b+c>0.
错误的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:根据对称轴方程,抛物线开口方向、与y轴交点坐标位置确定a、b、c的负号,根据图象知x=-1与x=1时所对应的y的负号进行判断.
解答: 解:如图所示,∵抛物线开口方向向下,
解:如图所示,∵抛物线开口方向向下,
∴a<0.
又对称轴-1<x=-
<0,
∴b<0,且b>2a,则2a-b<0.
故①正确;
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc<0.
故②正确;
如图所示,当x=1时,y<0,即 a+b+c<0.故③正确;
④如图所示,当x=-1时,y<0,即a-b+c<0.故④错误.
综上所述,错误的个数是1.
故选:A.
 解:如图所示,∵抛物线开口方向向下,
解:如图所示,∵抛物线开口方向向下,∴a<0.
又对称轴-1<x=-
| b |
| 2a |
∴b<0,且b>2a,则2a-b<0.
故①正确;
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc<0.
故②正确;
如图所示,当x=1时,y<0,即 a+b+c<0.故③正确;
④如图所示,当x=-1时,y<0,即a-b+c<0.故④错误.
综上所述,错误的个数是1.
故选:A.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则CD的长为( )
如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则CD的长为( )| A、6cm | B、4.8cm |
| C、2.4cm | D、1.2cm |
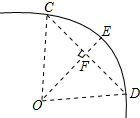 如图,一条公路的转弯处是一段圆弦(即图中
如图,一条公路的转弯处是一段圆弦(即图中
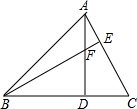 如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.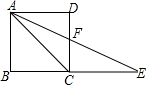 如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:①∠E=22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE;⑤AD:CE=1:2.其中正确的有
如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:①∠E=22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE;⑤AD:CE=1:2.其中正确的有