题目内容
10.已知二次函数y=2x2+1,若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1< y2.(填“>”、“=”或“<”).分析 抛物线开口向上,且对称轴为y轴.根据图象上的点的横坐标距离对称轴的远近来判断纵坐标的大小.
解答 解:∵二次函数y=2x2+1,
∴该抛物线开口向上,且对称轴为y轴.
∵点(-2,y1)与(3,y2)在二次函数y=2x2+1的图象上,
点(-2,y1)横坐标离对称轴的距离小于点(3,y2)横坐标离对称轴的距离,
∴y1<y2.
故答案为:<.
点评 本题主要考查对二次函数图象上点的坐标特征,二次函数的性质等知识点的理解和掌握,能求出对称轴和根据二次函数的性质求出正确答案是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
15.下列长度的各组线段,能组成直角三角形的是( )
| A. | 12,15,18 | B. | 12,35,36 | C. | 0.3,0.4,0.5 | D. | 2,3,4 |
19.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{20x}$ | B. | $\sqrt{7{a^2}}b$ | C. | $\sqrt{{a^2}-{b^2}}$ | D. | $\sqrt{\frac{a}{3}}$ |
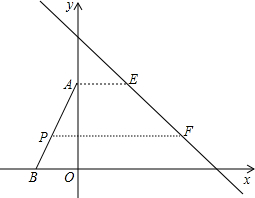 如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.
如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.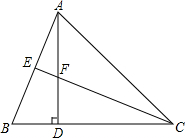 如图,在△ABC中,AD⊥BC于D,CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE⊥AB;(2)AE=BE.
如图,在△ABC中,AD⊥BC于D,CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE⊥AB;(2)AE=BE. 如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,求EC的长.
如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,求EC的长.