Question

5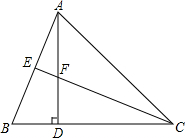．如图，在△ABC中，AD⊥BC于D，CE平分∠ACB分别交AB、AD于E、F两点，且BD=FD，AB=CF．求证：（1）CE⊥AB；（2）AE=BE．

Answer 1

分析 （1）根据直角三角形的全等证明和全等三角形的性质解答即可；
（2）根据角平分线的性质和全等三角形的判定和性质证明即可．

解答 证明：（1）∵AD⊥BC于D，
∴∠ADB=∠CDF=90°，
在Rt△ADB和Rt△CDF中，
$\left\{\begin{array}{l}AB=CF\\ BD=DF\end{array}\right.$，
∴Rt△ADB≌Rt△CDF（HL），
∴∠BAD=∠DCF，
在△AEF和△CDF中，
∠EAF=∠DCF，∠AFE=∠CFD，
∴∠AEC=∠CDF=90°
∴CE⊥AB，
（2）∵CE平分∠ACB
∴∠ACE=∠BCE，
又∵CE⊥AB，
∴∠AEC=∠BEC=90°，
$\begin{array}{l}在△ACE和△BCE中，\\ \left\{\begin{array}{l}∠ACE=∠BCE\\ CE=CE\\∠AEC=∠BEC\end{array}\right.\end{array}$，
∴△ACE≌△BCE（ASA），
∴AE=BE．

点评 本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA和HL，做题时，要根据已知条件结合图形进行思考．